Question 638925: The perimeter of a rectangle is 170 feet. If the length exceeds 5 times the width by 1 foot,then what is the area of the rectangle?
Found 2 solutions by josh_jordan, MathTherapy:
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula for finding the perimeter of a rectangle is P = 2L + 2W, where P is your perimeter, L is the length and W is the width.
The question says the Length exceeds the 5 times the width by a foot. In other words, Length = 5W + 1. We also know the perimeter is 170 feet, so 2L + 2W = 170. To solve, replace the L in the last sentence, for 5W + 1:
2(5W + 1) + 2W = 170
Using the distributive property, multiply 2 by what is in the parenthesis:
2(5W + 1) = 10W + 2
So now, our equation is:
10W + 2 + 2W = 170
Combine the like terms on the left side of the equal sign. This results in
12W + 2 = 170
Now subtract 2 from both sides of the equal sign:
12W + 2 - 2 = 170 - 2
This results in
12W = 168
Divide both sides of our equation by 12, that way we get W by itself
12W/12 = 168/12
This results in our width: W = 14 feet
Now, just replace the W with 14 in L = 5W + 1:
L = 5(14) + 1 = 71
Therefore, our length is 71 feet and our width is 14 feet. To verify, multiply 71 by 2 and 14 by 2 and add those results together. If they equal 170, our answer is correct: 2 x 71 = 142 and 2 x 14 = 28. 142 + 28 = 170, so our answer is correct.
Final Answer: Length = 71 feet and Width = 14 feet
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The perimeter of a rectangle is 170 feet. If the length exceeds 5 times the width by 1 foot,then what is the area of the rectangle?
Let width be W
Then length = 5W + 1
Since 2L + 2W = P, we now have: 2(5W + 1) + 2W = 170
10W + 2 + 2W = 170
12W = 168
W, or width = 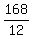 , or 14 ft , or 14 ft
Length = 5(14) + 1, or 71 feet ------ Substituting 14 for W
Area = 14(71), or  sq ft sq ft
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|