Question 638443: Two contestants run a 440-yard course. The first wins by 4 seconds when given a head start of 200 feet. They finish together when the first is given a head start of 40 yards. Find the speed of each in feet per second.
I tried to solve by using the formula D (distance)= s (speed) x t (time).
But I come up with two equations for each situation. Converting yards to feet: 440yards=1320 feet:
runner #1: s(t-4)=1120 (wins by 4 seconds)
runner #2: s(t)=1320
and for the second situation:
runner #1: s(t)=1200 (given a 40 yard=120feet head start: 1320-120=1200 feet).
runner #2 s(t)=1320
then solving for s: s=1320/t and substituting 1320/t(t-4)=1120 and solving for t, 1320t-5280=1120t, t=26.4 secs, then s=1320/t and s=1320/26.4= 50ft/sec.
Now, obviously a human cannot run at that speed, so this does not seem like a plausible answer, and I cannot figure out why I have four equations, I also tried to use different combinations but this didn't work either. So, I trust someone with better mathematical acumen can come up with a better solution. Thank you so kindly for trying to solve this problem. I look forward to the correct solution and appreciate your time and assistance.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two contestants run a 440-yard course. The first wins by 4 seconds when given a head start of 200 feet. They finish together when the first is given a head start of 40 yards. Find the speed of each in feet per second.
I tried to solve by using the formula D (distance)= s (speed) x t (time).
But I come up with two equations for each situation. Converting yards to feet: 440yards=1320 feet:
runner #1: s(t-4)=1120 (wins by 4 seconds)
runner #2: s(t)=1320
and for the second situation:
runner #1: s(t)=1200 (given a 40 yard=120feet head start: 1320-120=1200 feet).
runner #2 s(t)=1320
then solving for s: s=1320/t and substituting 1320/t(t-4)=1120 and solving for t, 1320t-5280=1120t, t=26.4 secs, then s=1320/t and s=1320/26.4= 50ft/sec.
Now, obviously a human cannot run at that speed, so this does not seem like a plausible answer, and I cannot figure out why I have four equations, I also tried to use different combinations but this didn't work either. So, I trust someone with better mathematical acumen can come up with a better solution. Thank you so kindly for trying to solve this problem. I look forward to the correct solution and appreciate your time and assistance.
Let the speed of the 1st runner be 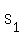 , and speed of 2nd, , and speed of 2nd, 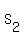
The course is 440 yards, or 1,320 feet
Since the 1st gets a headstart of 200 feet, then the 1st travels 1,320 – 200, or 1,120 feet
Time taken by 1st to go 1,120 feet, plus time won by, equals time taken by 2nd to go 1,320 ft, OR

 ---- Multiplying by LCD, ---- Multiplying by LCD,  ---- eq (i) ---- eq (i)
Since the 1st gets a headstart of 40 yards, or 120 feet, then the 1st travels 1,320 – 120, or 1,200 feet
Time taken by 1st to go 1,200 feet equals time taken by 2nd to go 1,320 ft, OR

 ---- Cross-multiplying ---- eq (ii) ---- Cross-multiplying ---- eq (ii)
Therefore,  ---- ----- Substituting ---- ----- Substituting 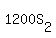 for for 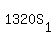 in eq (i) in eq (i)
 ----- Factoring out GCF, 4 ----- Factoring out GCF, 4



 ---- Factoring out GCF, ---- Factoring out GCF, 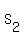

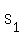 , or speed of 1st runner = , or speed of 1st runner =  ft/s ft/s
 ---- Substituting 20 for ---- Substituting 20 for 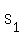 in eq (ii) in eq (ii)

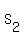 , or speed of 2nd runner = , or speed of 2nd runner = 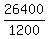 , or , or  ft/s ft/s
You can do the check!!
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|