Question 637336: solution and graph for this
y= 3 + 2 sin (2x - pi/2)
Found 2 solutions by josmiceli, jsmallt9:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can't solve a single equation with two variables. But you can graph it.
Graphing sin or cos equations is easiest when the equation is in the form:
y = C + A*sin(B(x - D)) where
C = Vertical shift
D = Phase (horizontal) shift
|A| = Amplitude
period = 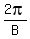
Notes:- The specific letters A, B, C and D are not important. Any letters can use used. You might have been taught an equation like this with different letters. What is important is what the letter represent. For example, the term that is separate from the sin term represents the vertical shift for the graph. It doesn't matter if it called C or J or Q or anything else, the separate term is the vertical shift. The same can be said about the A, B and D. It's not important what they are called. It is the position they have in the equation and the role they play in the graph which are important.
- The separate term can be put in the back (because addition is Commutative):
y = A*sin(B(x - D)) + C
I prefer it in front because then there is no way for the C to be mistakenly considered part of the argument of sin. - Some books/teachers teach a different form:
y = C + A*sin(Bx - D)
where the B is not a factor of the argument. It is just the coefficient of x. The only advantage to this form is that it is little simpler. But it complicates the interpretation of D and its use in graphing.
Now let's look at your equation:

This is not in preferred form. So I'll factor out the 2 in the argument:

Now we can see that
A = 2 so the amplitude is |2| = 2
B = 2 so the period = 
C = 3 so the vertical shift is 3
D =  so the phase shift is so the phase shift is 
From this we can draw a graph easily. This is usually done with steps like...- Draw a dotted horizontal line at the vertical shift. For this equation, a dotted line at y = 3
- From this dotted line go up and down by the amplitude and draw two more horizontal dotted lines. For this equation, we would go up 2 from 3 and draw a horizontal dotted line at y = 5 and we would go down 2 from 3 and draw a horizontal dotted line at y = 1.
- Find the following points on the x-axis:
- (phase shift, 0)
- (phase shift + period, 0)
- (phase shift - period, 0)
For our equation these would be:
( , 0) , 0)
(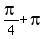 , 0) or ( , 0) or ( , 0) , 0)
(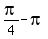 , 0) or ( , 0) or (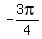 , 0) , 0)
Note: Many people like to find additional points:
(phase shift + period/4, 0)
(phase shift + period/2, 0)
(phase shift + 3*period/4, 0)
because every 1/4 cycle a critical point (maximum, minimum, or midpoint) occurs. - Note: We have not actually started the graph yet. The dotted lines and the points we've found are just to guide us as we start drawing the actual graph. Since sin's start their cycle halfway between the maximum and the minimum we need to find the point (phase shift, vertical shift). In our case, (
 , 3) This is where we start drawing the graph. , 3) This is where we start drawing the graph. - Sin's proceed from this midpoint and proceed next to its maximum. So 1/4 cycle later we should be at the maximum, y=5. 1/4 cycle after that we are back to the midpoint, 1/4 of a cycle after that we are at the minimum, y = 1 and 1/4 cycle after that we are back at the start of the cycle. So try to draw a smooth sin curve that starts from (
 , 3) and ends at ( , 3) and ends at ( , 3). If you found the "extra" points back at step 3, you can make sure the curve reaches the maximum, returns to the midpoint and reaches the minimum at the right places and your graph will look much better. , 3). If you found the "extra" points back at step 3, you can make sure the curve reaches the maximum, returns to the midpoint and reaches the minimum at the right places and your graph will look much better. - Repeat the last step going backwards (minimum first) from (
 , 3) and ends at ( , 3) and ends at (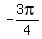 , 3). (This is not required but it is recommended.) , 3). (This is not required but it is recommended.)
Your graph should look something like:

|
|
|