Question 637274: Find the sum of the first ten terms of the the series 1+4+16+64+256
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The terms are in a geometric sequence, or geometric progression.
Each term is the previous one multiplied times  . .
You may be studying geometric sequences, also called geometric progressions.
The symbols and names used vary a little from place to place, from book to book, and from teacher to teacher, so the symbols, and formulas may look different, but the idea is the same. I will use a popular choice for terms, symbols, and formulas. Keep in mind that your book/teacher may use slightly different ones.
THE GENERAL THEORY (what the book may say):
In a geometric sequence, or geometric progression, the term number  and the number and the number 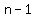 (the previous one) are related by the recurrence formulas (the previous one) are related by the recurrence formulas
 or or  , ,
Where  is the tern number is the tern number  , ,
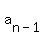 is the previous term, and is the previous term, and  is the common ratio. is the common ratio.
The term number  can be calculated from the first term and the common ratio, using the explicit formula can be calculated from the first term and the common ratio, using the explicit formula

The sum of the first  terms, terms,  + ... + + ... +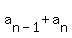
can be calculated as

The formula can be deduced as follows:
 + ... + + ... +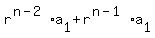 , so , so
 + ... + + ... +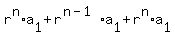
Subtracting one equation from the other, a lot of terms cancel, and you have
 --> --> 
Then, dividing both sides by 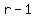 , we get , we get
 --> --> 
Someone discovered that formula. I just remember the trick and re-discover the formula every time, because I do not need to use it often, and do not remember it.
THE SOLUTION TO THE PROBLEM:
 , ,  , , 
Applying the formula  , we get , we get

|
|
|