SOLUTION: If log2 base 10=0.13010& log3 base 10=0.4771 evaluate log 4.5 base 10

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: If log2 base 10=0.13010& log3 base 10=0.4771 evaluate log 4.5 base 10      Log On


   

Question 636996: If log2 base 10=0.13010& log3 base 10=0.4771 evaluate log 4.5 base 10
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
First of all, log(2) is close to 0.3010, not 0.13010. I think you have an extra 1 in your post. I will solve this using 0.3010. If you really think you should be using 0.13010, then you will have to make your own calculation at the end with this other number.

Finding logarithms without a calculator involves finding a way to express the desired log in terms of logs you know.

In this problem you were told what log(2) and log(3) are. Plus, you should know on your own what the base 10 log of any power of 10 is (log(10) = 1, log(100) = 2, log(1000) = 3, log(1/10) = -1, etc.)

So for this problem, you are looking for a way to express log(4.5) in terms of log(2), log(3) and/or the log of any power of 10. And how does one change the log of one number into an expression of logs of other number(s)? Answer: Using the properties of logarithms, in particular:
  • log%28a%2C+%28p%2Aq%29%29+=+log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29
  • log%28a%2C+%28p%2Fq%29%29+=+log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29
  • q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29
TO summarize these properties, logs of products, quotients or powers can be rewritten in terms of logs of the "parts" (factors, dividend/numerator, divisor/denominator, base, exponent).

So we can solve this problem if we can find a way to express 4.5 as a product, quotient and/or power of 2's, 3's and/or powers of 10. Finding a solution takes some trial and effort. There are often more than one way to do these problems. One way to express 4.5 I can see without much effort is:
4.5+=+4%261%2F2+=+9%2F2+=+3%2A3%2F2

Now that we have expressed 4.5 in terms of 2's and 3's, we can use the properties and the given values of log(2) and log(3) to find our answer:
log%28%284.5%29%29
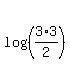
log%28%283%2A3%2F2%29%29
Now we can use the quotient property (the second one listed above) to rewrite this:
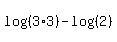
log%28%283%2A3%29%29+-+log%28%282%29%29
Now we can use the product property (the first one listed above) to rewrite the first log:
log%28%283%29%29+%2B+log%28%283%29%29+-+log%28%282%29%29
We can now use the given values to evaluate this expression:
0.4771 + 0.4771 - 0.3010
0.6532

So log(4.5) = 0.6532.