Question 636832: The distance between city A and B is 90 kilometers. At the same time, a car and a motorcycle left from city A to city B. The motorcycle drove at a constant speed the entire drive and the car passed 1/3 of the drive 30 kilometers per hour faster than the motorcycle's speed, stopped for half an hour, and then continued the drive at a speed 20% slower than the speed driven in the first 1/3 of the drive. The car arrived 15 minutes before the motorcycle to city B (they drove the same distance). What was the speed of the motorcycle?
This is supposed to be easy, I just keep messing up somewhere.
I know Distance=Speed*Time
The motorcycle's speed is x, and the time is 90/x (because the distance is 90)
The car's speed is x+30, and the time is 30/x+30 (because 1/3 of 90 is 30)
Then the speed is .80(x+30) and the time is 60/.8x+24 (the remaining distance being 60 km)
but the car stopped for half an hour, and then arrived 15 minutes before the motorcycle, so I only add 1/4 of an hour to the time in the second equation..
After this step I keep getting stuck... Could you please help me finish?
Thanks so much! I don't know what I would do without your help!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The distance between city A and B is 90 kilometers.
At the same time, a car and a motorcycle left from city A to city B.
The motorcycle drove at a constant speed the entire drive and the car passed
1/3 of the drive 30 kilometers per hour faster than the motorcycle's speed,
stopped for half an hour, and then continued the drive at a speed 20% slower
than the speed driven in the first 1/3 of the drive.
The car arrived 15 minutes before the motorcycle to city B (they drove the same distance).
What was the speed of the motorcycle?
This is supposed to be easy, I just keep messing up somewhere.
I know Distance=Speed*Time
The motorcycle's speed is x, and the time is 90/x (because the distance is 90)
The car's speed is x+30, and the time is 30/x+30 (because 1/3 of 90 is 30)
Then the speed is .80(x+30) and the time is 60/.8x+24 (the remaining distance being 60 km)
--------------------------------------------
From what I see here, you have a time equation:
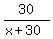 + + 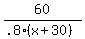 + .5 = + .5 = 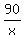 - .25 - .25
we can simplify the 2nd fraction, divide .8 into 60 and we have
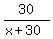 + + 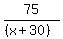 + .5 = + .5 = 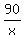 - .25 - .25
subtract .5 from both sides, add fractions with same denominator and we have
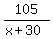 = = 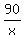 - .75 - .75
Multiply by x(x+30) to clear denominators, results:
105x = 90(x+30) - .75x(x+30)
105x = 90x + 2700 - .75x^2 - 22.5x
Arrange as a quadratic equation on the left
.75x^2 + 22.5x - 90x + 105x - 2700 = 0
.75x^2 + 37.5x - 2700 = 0
Simplify, divide by .75. results
x^2 + 50x - 3600 = 0
This will factor to
(x+90)(x-40) = 0
The positive solution
x = 40 mph is the motorcycle speed
:
Check this out in the original time equation
|
|
|