Question 636765: Please help. Due tomorrow.
1.)A box is to be formed by cutting squares measuring 2 cm on a side from a square piece of cardboard and then folding the sided. If the volume of the box is to be 392 cm squared, what is the original size of the cardboard?
2.)Manuel is constructing a model house. He wants each window to have an area of 315cm squared, and he wants the length of each window to be 6 cm more than the width. What are the dimensions of each window?
3.)A circle has a radius of 20 cm. By how much must the radius be increased so that the area will increase to 144 pie cm squared?
4.)An airplane flies 900 miles against a headwind if 25 miles per hour. The plane took 15 minutes longer for this flight than with a tailwind of 25 miles per hour. How fast could the plane fly in still air?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.)The box is formed by cutting squares measuring 2 cm on a side from a square piece of cardboard That looks like this, with the cutting lines marked in red:
 The folding lines, shown in blue, show the central square that will be the base of the box. The folding lines, shown in blue, show the central square that will be the base of the box.
The box sides (the folded flaps on all four sides) will 2 cm high, and that will be the height of the box.
The volume of the box,  , is the surface area of the base, , is the surface area of the base,  , times the height, , times the height,  of the box. of the box.
 , so , so 
If the volume of the box is to be 392 cubic centimeters, then the surface area of the base of the box is
 =(392 cubic centimeters)/(2 centimeters)= =(392 cubic centimeters)/(2 centimeters)= =196 square centimeters. =196 square centimeters.
What is the original size of the cardboard?
THE FIFTH GRADER SOLUTION:
The area of the square that is the base of the box is side of the base of the box squared.
 , so the base of the box is a 14 cm by 14 cm square. , so the base of the box is a 14 cm by 14 cm square.
With 2 cm of cardboard to each side (4 extra cm), the width of the square piece of cardboard, before cutting was

IF YOU KNOW ENOUGH ALGEBRA TO COMPLICATE THE PROBLEM:
You start by saying, let  cm be the length of each side of the square piece of cardboard, which looks like this, with the cutting lines marked in red: cm be the length of each side of the square piece of cardboard, which looks like this, with the cutting lines marked in red:
 The folding lines, shown in blue, show the central square that will be the base of the box. The folding lines, shown in blue, show the central square that will be the base of the box.
That length of each side of that square base of the box is
 cm cm
That surface area of the base of the box (in square cm) is

The height of the box is 2 cm.
The volume of the box (area of the base times height) is
 square centimeters. square centimeters.
If we are smart, we divide both sides by 2 now to get a simpler equation:
 --> --> 
Then we subtract 196 from both sides, to get a quadratic equation in standard form.
 --> --> 
To solve that quadratic equation, if we are not good at factoring, we have to "complete the square", or use the dreaded quadratic formula.
If we are good at factoring, we realize that 
and find that the solutions are  and and  . .
Since the length of the side of the original square piece of cardboard cannot be a negative number, the only solution is
The length of the side of the original square piece of cardboard is  cm. cm.
2.)
THE FIFTH GRADER SOLUTION:
The fifth grader may factor to find that the prime factorization of 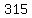 is is
 , and would rearrange that to find , and would rearrange that to find
 to figure out that the windows are 15 cm by 21 cm. to figure out that the windows are 15 cm by 21 cm.
That fifth grader is smart and lucky, but we should try to use algebra, because the fifth grader approach would not work for a similar problem where the answers were not integers. (However, problems are often rigged so they have integer answers, and it is good to have a smart fifth grader around, so he/she can check your algebra answers).
THE ALGEBRA SOLUTION:
Let the width of each window be  cm. cm.
Then the length of each window (in cm) would be 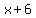 . .
The area (in square centimeters) of each window, calculated multiplying length times width, would be

We work with that equation to transform it into a quadratic equation in a form that we like better.
 --> -->  --> --> 
We can solve it by "completing the square", or by factoring, of by using the quadratic formula.
Completing the square:
 --> -->  --> -->  --> -->  --> --> 
The two solutions would be:
 --> -->  , which does not make sense, and , which does not make sense, and
 --> -->  --> --> 
So the width of the windows is  cm and the length is cm and the length is  cm. cm.
Factoring:
From  we realize that we realize that
since  and and  , ,
 , so we re-write the equation as , so we re-write the equation as

One of those factor must be zero, and realize that the solution coming from
 --> -->  gives us a valid window width of gives us a valid window width of  cm, for a length of cm, for a length of  cm. cm.
On the other hand, making the other factor zero, leads to an invalid solution:
 --> -->  , because the width of the windows cannot be a negative number. , because the width of the windows cannot be a negative number.
3.)The area,  of a circle of radius of a circle of radius  can be calculated as can be calculated as 
The area (in square centimeters) of circle with a radius of 20 cm is  . .
That is more than 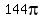 , so either , so either
there is a typo somewhere in the problem, or
it is a trick question, where they call a decrease in area from
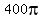  down to down to 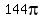  is called is called
an increase of  - -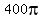  = =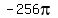  . .
If the area of a circle with radius  is is
 , dividing both sides by , dividing both sides by  , we get , we get
 --> -->  --> --> 
Since 
I would say that the radius must be increased  so that the area will increase (by so that the area will increase (by 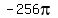  ) to 144 pie cm squared? ) to 144 pie cm squared?
4.)If the speed of an airplane relative to the air is  miles per hour, miles per hour,
the plane will move at  miles per hour with respect to the ground in still air. miles per hour with respect to the ground in still air.
With a tail wind of  miles per hour, the same airplane will move at miles per hour, the same airplane will move at 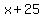 miles per hour with respect to the ground. miles per hour with respect to the ground.
Against a wind of  miles per hour, the same airplane will move at miles per hour, the same airplane will move at 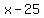 miles per hour with respect to the ground. An airplane flies 900 miles against a headwind of 25 miles per hour. miles per hour with respect to the ground. An airplane flies 900 miles against a headwind of 25 miles per hour.
We know that speed, time and distance are related like this:
 <--> <-->  <--> <--> 
If we want to figure how long a trip will take, we divide distance by speed.

If the plane took 15 minutes longer to fly the same 900-mile distance against that wind than with the wind, the equation relating the times, in hours is

To get rid of denominators, we multiply both sides of the equation time 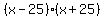





Adding  to both sides, or subtracting to both sides, or subtracting  from both sides, we get from both sides, we get

 --> -->  --> -->  --> -->  --> -->  --> -->  miles per hour. miles per hour.
|
|
|