|
Question 636041: Write a rational function f that has the following characteristics.
a) Vertical asymptote: x=2
b) Slant asymptote: y=3x+1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please try to post your problems in an appropriate category. This problem has nothing to do with Trigonometry. This misdirected posting could be the reason you have not gotten a response earlier. Many tutors only look at problems in the categories they like. So tutors that like rational function problems may have never see this problem. It is to your advantage to post in an appropriate category.
Vertical asymptotes of a rational function, if any, occur for x values that make the function's denominator equal to zero. Assuming the x=2 is supposed to be the only vertical asymptote, then the denominator of f could be any of the following:
x-2

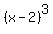
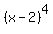
etc.
Since multiple denominators are possible, there are multiple correct answers to this problem. (This is probably why the problems says "write a function ..." instead of "write the function ...") Let's be easy on ourselves and pick the simplest one: x-2. So at this point:
f(x) = something/(x-2)
As for the slant asymptote, let's think about how you would find one. (I have to assume that you have found slant asymptotes for a given function already.) Once we remember how slant asymptotes are found we will then try to go backwards from the asymptote to the function.
To find a slant asymptote you divided the numerator of the function by its denominator, using either long or synthetic division. This division resulted in the quotient being in the form mx + b and a remainder fraction. The quotient part was the slant asymptote and the denominator of the remainder fraction was the same as the denominator of the original function.
For our particular function f, we want the quotient part (the slant asymptote) to be 3x + 1 and we want the denominator of the remainder fraction to be x-2, like f's denominator. So function f, divided out, should be:
f(x) = 3x + 1 + something/(x-2)
The numerator of the remainder fraction can be anything as long as it is not zero and it's degree is less than the degree of the denominator. Our denominator, x-2, has a degree of 1. So we need a numerator with a degree of 0 (IOW, a number, no variable terms). So our numerator in the remainder fraction can be any non-zero number. Any such number will do. Let's be easy on ourselves again and pick a number that's easy to work with, like 1. So now our function, divided out, looks like:
f(x) = 3x + 1 + 1/(x-2)
Now how do we go backwards from this to the general form for rational functions, polynomial over polynomial? We got to
f(x) = 3x + 1 + 1/(x-2)
by dividing out f's numerator by x-2 so we can go backwards and find f's numerator by multiplying 3x + 1 + 1/(x-2) by (x-2). (Another way to look at this is to get all the denominators the same and then add.)
 This is f's numerator. This is f's numerator.
So one possible f(x) with the given asymptotes is:

|
|
|
| |