Question 635834: Solve the following exponential equation.?
49^x+7^(x-1)-18=0
Could someone please just get me started?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
You only asked for help getting started. But this problem is challenging so I don't really know how much help you will need. So as soon as you figure what's going on, just stop reading.
The first key to solving this equation is to "see" a  in both in both 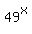 and and 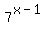
The  in in 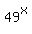 is probably easier to see: is probably easier to see:

To rewrite 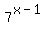 in terns of in terns of  we will need to extract the "-1". Think of how the -1 may have gotten there to begin with. What operation causes one to subtract exponents? Answer: When you divide exponential terms with the same base: we will need to extract the "-1". Think of how the -1 may have gotten there to begin with. What operation causes one to subtract exponents? Answer: When you divide exponential terms with the same base:

Now let's see what our equation looks like after we rewrite the first two terms in terms of  : :

The equation, written this way, is in what is called "quadratic form". It can be easier to see this if we use a temporary variable:
Let 
Then our equation, written with q's, is:

This is clearly a quadratic equation. We can continue, for a while, with the temporary variable.. First let's get rid of the fraction by multiplying by 7:

This won't factor so we'll use the Quadratic Formula:

Simplifying:




which is short for:
 or or 
We've solved for q. But we don't care about q. We care about x. So now we'll substitute back in for q:
 or or 
And solve for x.
I hope it is obvious that the fraction in the second equation, 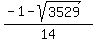 , will be negative. (If it is not obvious, then work it out on your calculator.) And it is not possible for any power of 7 to be negative. So the second equation above has no solutions. The only solutions we will get will come from the first equation. , will be negative. (If it is not obvious, then work it out on your calculator.) And it is not possible for any power of 7 to be negative. So the second equation above has no solutions. The only solutions we will get will come from the first equation.
(Note: As a teacher I prefer my students to find exact solutions unless I tell them to find a decimal approximation. Your problem doesn't mention decimal approximations so I'm assuming that an exact solution is desired. If I'm wrong then you might want to use your calculator on the first equation above and get a decimal for the right side before proceeding.)
To solve

we will be using logarithms. Any base of logarithms can be used. If we choose base 7 logarithms then we will get the simplest possible expression for the answer. If we choose a base of logarithm that your calculator "knows", base 10 (log) or base e (ln), then we get an less simple but still exact expression that can be easily turned into a decimal approximation if needed/wanted. I'm going to use ln:

Now we use a property of logarithms,  , to move the exponent out in front: , to move the exponent out in front:

And last of all, divide both sides by ln(7):

Big and ugly, yes, but it is an exact expression for the solution to your equation.
P.S. Can you see how using base 7 logs would lead to a simpler expression? Try it and see.
P.P.S. After you've done a few of these "quadratic form" equations you will no longer need to use a temporary variable. You will see how to go directly from

to

to

etc.
|
|
|