|
Question 63552: Use Pascal's Triangle to expand each binomial.
(x+y)^8
Found 2 solutions by joyofmath, praseenakos@yahoo.com:
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use Pascal's Triangle to expand each binomial.
(x+y)^8
Here's the first 9 rows of Pascal's triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
The 9th row gives us the coefficients for 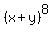 : :
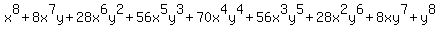
Answer by praseenakos@yahoo.com(507)   (Show Source): (Show Source):
You can put this solution on YOUR website! QUESTION;
Use Pascal's Triangle to expand each binomial.
(x+y)^8
===============================================================================
ANSWER:
Pascal's Triangle.
It is a triangle of numbers, which is given below:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
Each number in the triangle is the sum of two above. For example, the 6 on line 5 is the sum of the pair of 3's above. So the next line is
1, 10 (1 + 9), 45 (9 + 36), 120 (36 + 84), etc.
Study these numbers and see if you can figure what the next line should be before reading on . . .
Your question.
(x+y)^8
Here we have to expand the 8th power.
Ninth raw in Pascal's triangle gives the coefficient of the terms in the resulting expansion.
that means, the coeffients are, 1 8 28 56 70 56 28 8 1
Now write the variable part like this,
x^8
x^7 * y
x^6 * y^2
x^5 * y^3
x^4 * y^4
x^3 * y^5
x^2 * y^6
x^1 * y^7
y^8
(power of the first term will decrease while power of second term will increase till it is 8.)
(x+y)^8 = 1x^8+ 8x^7 y^1+ 28x^6 y^2 + 56 x^5 y^3+ 70x^4 y^4+56x^3y^5 +
28x^2 y^6+ 8x^1 y^7+ 1x^8
= x^8+ 8x^7 y^1+ 28x^6 y^2 + 56 x^5 y^3+ 70x^4 y^4+56x^3y^5 +
28x^2 y^6+ 8x^1 y^7+ x^8
Hope you understood.
Regards.
Praseenakos@yahoo.co.in
|
|
|
| |