Question 635324: There a three exams in a marking period. A student recevied grades of 75 and 81 on the first two exams. What grade must the student earn on the last exam to get an average of no less than 80 for the marking period
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the grade in the last exam. be the grade in the last exam.
The average is
(75+81+ )/3= )/3=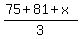
(Note how the long horizontal fraction line includes hidden, invisible parentheses).
For an average of no less than 80, we need

We start working with that inequality to figure out what are the requirements for  : :
 --> -->  --(multiplying both sides times 3)--> --(multiplying both sides times 3)-->  --> --> 
We are almost there. Now we subtract 156 from both sides (or you could say we add 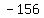 to both sides). to both sides).
 --> -->  --> --> 
Note 1:
For inequalities, you can get an equivalent inequality by
adding/subtracting the same number (or algebraic expression) to both sides,
multiplying/dividing by the same POSITIVE number both sides.
If you must multiply/divide by a negative number, as in
-x<-5 ----> x>5
flip the inequality sign at the same time, because multiplying times (-1) is flipping the whole number line.
Note 2:
If using mental math for the same problem, you could say:
On the first test, I was 5 short of the 80 grade I wanted,
so I need to make up those 5 points between the next two tests.
I recovered one (1) point with the 81 in the second test, because 81 is 1 more than the 80 I wanted.
So I still need 4 more points over 80 on the last test to make up for the 5 points missed in the beginning.
|
|
|