Question 635320: The dimensions of a rectangle are such that the length is 7in. more than the width. If the length were doubled and the width decreased by 3in. then the area would increase by 90in.sq. What are the length and width of the rectangle?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the width of the rectangle, in inches. be the width of the rectangle, in inches.
The length of the rectangle( in inches) is 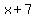 . .
The area is the product of length times width, so it is
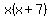 square inches. square inches.
The modified rectangle has a length (in inches) of 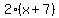 , ,
and a width (in inches) of  . .
The area (in square inches) of the modified rectangle is
 , ,
and that new area is 90 square inches more than the area of the original rectangle.
So the equation, in its most complicated form (just in case the teacher wants that), is

Let's un-complicate and solve.
 --> -->  (associative property) (associative property)
(We are so familiar with he associative property that we probably could write it as
 in the un-complicated no-parentheses form from the start). in the un-complicated no-parentheses form from the start).
Form there, we multiply the expressions with  to get to get

Collecting like terms, we get

We multiply further to get

Then we add 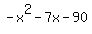 to both sides (or subtract to both sides (or subtract 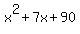 , same thing), to get , same thing), to get

That simplifies to our quadratic equation:

If we are good at factoring, we can easily figure that
 and then we would re-write the equation as and then we would re-write the equation as
 , with solutions , with solutions  and and 
The width of the rectangle is  inches and the length is inches and the length is  inches. inches.
Verification:
The area of the rectangle is (11 inches)(18 inches) = 198 square inches.
The length of the modified rectangle is
2(18 inches) = 36 inches, and the new width is
11 inches - 3 inches = 8 inches.
Then, the area of the modified rectangle is
(8 inches)(36 inches) = 288 square inches,
which is 90 square inches more than the original 198 square inches,
because 198+90=288.
|
|
|