Question 635193: How to find log (5,512) ? i.e., log 512 to the base 5.. log 2 base 10 =0.3010 and log 3 base 10=0.4771 are provided.. Help me to solve this prob without using log table and calculator..
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!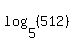 
The logs we've been given are base 10 logs. This suggests that we should rewrite our base 5 log in terms of base 10 logs. The base conversion formula is:
 . Using this we can change our base 5 log into an expression of base 10 logs:
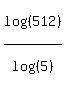
Now our task is to figure out how to express log(512) and log(5) in terms of the base 10 logs we know. More specifically we want to express 512 and 5 as a product, quotient or power of a number whose log we know.
We know log(2) and log(3) because they were given to us. But we also get to use log's that we are supposed to know without them having been given to us. In this case, since we're working with base 10 logs, we should be able to figure out the base 10 log of any power of 10:
log(10) = 1, log(100) = 2, log(1000) = 3, etc.
log(1) = 0, log(1/10) = -1, log(1/100) = -2, etc.
 ,  ,  , etc.
So, in short, we are now looking to express 512 and 5 as products, quotients of powers of 2's, 3's and/or any power of 10.
As it turns out, the 512 might be the easier one. With a little effort we can find the  . For the 5 we can't use 2+3. It has to be a product, quotient or power, not a sum. For the 5 we will use 10/2, the quotient of a power of 10 and one of the numbers whose logs we were given. So now we have:
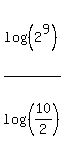
Now we use properties of logarithms to rewrite these logs in terms of log(2) and log(10). The the log in the numerator we will use a property of logarithms,  , move the exponent out in front. In the denominator we will use another property of logarithms,  , to split the 10 and th e2 into separate logs:
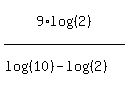
Now we replace all the logs with the values ww know that they are:
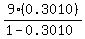
And simplify:
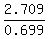
3.87553648
So 
|
|
|
