Question 635082: Hi, I'm terribly stuck with this question:
The angle x satisfies the equation 2tan(x)^2-5sec(x)-10=0, where x is in the second quadrant. Find the value of sec(x)
Thankyou :)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Solving Trig equations like this usually involves three stages:- Use algebra and/or Trig properties to transform the equation into one or more equations of the form:
TrigFunction(expression) = number - Find the general solution for the equation(s) from stage 1. Trig. functions are periodic so there are usually an infinite number of solutions to these equations. The general solution expresses these infinite solutions.
- Often these problems ask for a specific solution, like "Find the smallest positive solution to..." or "Find all solutions that are between p and q". To find specific solutions, you use the general solution.
Let's see this in action...
1. Transform.
With two different functions, tan and sec, we probably should be looking to find a way to change tan to sec, sec to tan or both of them to some other function. Fortunately there is a Trig. property that connects tan and sec:

If we solve this for 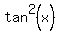 : :

then we can substitute in for the 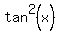 in our equation: in our equation:

Note the use of parentheses. This is very important when making substitutions, especially when you are substituting in a multiple-term expression like we are now.
Simplifying the equation we get:


We can get our desired form by factoring this:
2sec(x)+3)(sec(x)-4) = 0
(If you have trouble seeing how this factored, then look at sec(x) as a variable. Let's say q = sec(x). Then our equation is  . I hope you can see that this would factor into (2q+3)(q-4) = 0. And this, I hope, helps you understand how . I hope you can see that this would factor into (2q+3)(q-4) = 0. And this, I hope, helps you understand how  factored into 2sec(x)+3)(sec(x)-4)=0 factored into 2sec(x)+3)(sec(x)-4)=0
Now we use the Zero Product Property:
2sec(x)+3) = 0 or sec(x)-4 = 0
Solving these for sec(x) we get:
sec(x) = -3/2 or sec(x) = 4
We have now transformed the original equation into two equations of the desired form. (Note: Don't be discouraged. This first stage is usually the longest and hardest stage.)
2. Find the general solution.
Since a) sec and cos are reciprocals of each other; and b) we are usually not as familiar with sec values as we are with cos values; and c) there is no "sec" button on our calculator, we are going to rewrite these equations in terms of cos:
cos(x) = -2/3 or cos(x) = -1/4
Now, as cos's, we should be able to recognize that neither -2/3 nor -1/4 are special angle values for cos. So x is not a special angle. We will need our calculators.
First let's look at
cos(x) = -2/3
We will use our calculator to find the reference angle. (Note: Do not use a negative number when finding reference angles!) So we will find:
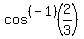
on our calculator. If we have made sure it is set to radian mode we should get a reference angle of 0.84106867 radians. And since cos(x) is -2/3, we know that x must terminate in the 2nd or 3rd quadrants (because that is where cos's are negative. Combining these we get:
 (for the 2nd quadrant) (for the 2nd quadrant)
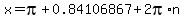 (for the 3rd quadrant) (for the 3rd quadrant)
Now we will deal with cos(x) = -1/4 (in much the same way as above:

Again, x trermiantes in the 2nd or 3rd quadrant because cos(x) is negative. So we get:
 (for the 2nd quadrant) (for the 2nd quadrant)
 (for the 3rd quadrant) (for the 3rd quadrant)
The general solution (the set of all possible solutions to your equation) is all four of the equations we have found:

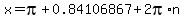


(Note: The "n" in these equations is a placeholder for any integer. To get specific x values, you replace "n" with an integer. Each integer value for n will result in an x value that is a solution to our equation. Some books/teachers use a different letter, like "k". The specific letter used is not important. What is important is that no matter what letter is used, it is a placeholder for an integer.)
3. Find the specific solution(s).
Your problem states we only want x's that terminate in the 2nd quadrant. So we will use only the equations that give us 2nd quadrant x's:


Since the problem only requests solutions that are in the second quadrant, our "specific solution" is the two equations above. By replacing the n's in these two equations we get x's that are solutions and do terminate in the 2nd quadrant.
P.S. Since our reference angles are already decimal approximations, feel free to replace  with a decimal and then simplify. with a decimal and then simplify.
|
|
|