Question 634881: Find the angles of 0 degree \< x \< 360 degrees of the equation cos 4x - cos 2x = 0
Found 2 solutions by jsmallt9, Alan3354:
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! cos(4x)-cos(2x) = 0
Solving Trig equations like this usually involves three stages:- Use algebra and/or Trig properties to transform the equation into one or more equations of the form:
TrigFunction(expression) = number - Find the general solution for the equation(s) from stage 1. Trig. functions are periodic so there are usually an infinite number of solutions to these equations. The general solution expresses these infinite solutions.
- Often these problems ask for a specific solution, like "Find the smallest positive solution to..." or "Find all solutions that are between p and q". To find specific solutions, you use the general solution.
Let's see this in action...
1. Transform.
If the transformation needed is not immediately obvious, there are steps you can take:- Use Trig. properties to make all the arguments the same.
- Use Trig. properties to reduce the number of functions in the equation. Often we will transform tan's, cot's, sec's and csc's into sin's and/or cos's.
With our equation we have only one function, cos, but we have two arguments, 4x and 2x. So let's try matching the arguments. We could change the 4x to 2x or the 2x to 4x or both of them to some third expression. The easiest for this problem, IMHO, is to change the 4x to 2x so this is what we will do.
By changing 4x to 2x we are, in effect, dividing the argument in half. This is a job for the "Double Angle" formulas. (I know using "Double Angle" formula to halve something sounds wrong but it is actually correct.) Let's look at an example:
sin(2x) = 2sin(x)cos(x) is the double angle formula for sin. It can be used to halve any sin's argument:
sin(6x) = 2sin(3x)cos(3x)
sin(20x) = 2sin(10x)cos(10x)
sin(12.6x) = 2sin(6.3x)cos(6.3x)
etc.
Once you learn that these formulas are patterns and that the x's, A's and B's in them can be replaced with any expression, you will have made a big step forward in knowing how to use them.
So we will use a cos(2x) formula to change cos(4x) into an expression with arguments of 2x. With cos(2x) we have three variations:They will all work. You can choose any one of them. But I am going to choose the second one because it has just cos in it. So not only will this match the arguments, it will keep the equation as a "cos-only" equation. Replacing cos(4x) with 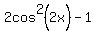 we get: we get:

This equation is a quadratic equation in terms of cos(2x). One side is already zero. All we have to do is rearrange the terms and then factor:

Now we factor. If you have trouble seeing this, then it might help to use a temporary variable. Let q = cos(2x). Then  and the equation becomes: and the equation becomes:  It is probably easier to see the factoring when it is written this way. It is probably easier to see the factoring when it is written this way.

Then from the Zero Product Property:
 or or 
Now we solve for cos(2x):
 or or 
 or or 
We have now transformed the original equation into two equations of the desired form. (This is usually the longest, hardest part of these problems.)
2. Find the general solution.
We should recognize that both -1/2 and 1 are special angle values for cos. So we will not need our calculators. Let's start with

We should know that the reference angle for a cos of 1/2 is 60 degrees. (Note: Don't use negatives to find reference angles!). The fact that it is -1/2 tells use that the angle, 2x, must terminate in the 2nd or 3rd quadrant (since that is where cos's are negative. Combining a reference angle of 60 with 2nd and 3rd quadrants we should get:
2x = 180 - 60 + 360n (for the 2nd quadrant)
2x = 180 + 60 + 360n (for the 3rd quadrant)
These simplify to
2x = 120 + 360n
2x = 240 + 360n
Now solve for x by dividing by 2:
x = 60 + 180n
x = 120 + 180n
(Note how the 360n gets divided by 2, too.)
Now we'll do the general solution to cos(2x) = 1. The only place cos is 1 is at zero degrees. So we just get one equation:
2x = 0 + 360n
Dividing by 2 we get:
x = 0 + 180n
So our general solution is all three equations:
x = 60 + 180n
x = 120 + 180n
x = 0 + 180n
(Note: The "n" in these equations is a placeholder for any integer. To get specific x values, you replace "n" with an integer. Each integer value for n will result in an x value that is a solution to our equation. Some books/teachers use a different letter, like "k". The specific letter used is not important. What is important is that no matter what letter is used, it is a placeholder for an integer.)
3. Find the specific solution(s).
This is where we actually replace the n's in the general solution equations. We keep trying different n's until we feel we have found all the specific solutions. I'm assuming that "0 degree \< x \< 360 degrees" means
 . So we are looking for all x's between 0 and 360, including 0 and 360. . So we are looking for all x's between 0 and 360, including 0 and 360.
From x = 60 + 180n:
When n = 0, x = 60
When n = 1, x = 240
When n = 2 or larger, x is more than 360 (too big for  ) )
When n is negative, x is negative (too small for  ) )
From x = 120 + 180n:
When n = 0, x = 120
When n = 1, x = 300
When n = 2 or larger, x is more than 360 (too big for  ) )
When n is negative, x is negative (too small for  ) )
From x = 0 + 180n:
When n = 0, x = 0
When n = 1, x = 180
When n = 2, x = 360
When n = 2 or larger, x is more than 360 (too big for  ) )
When n is negative, x is negative (too small for  ) )
So all our specific solutions, in order from lowest to highest, are:
0, 60, 120, 180, 240, 300 and 360.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the angles of 0 degree \< x \< 360 degrees of the equation cos 4x - cos 2x = 0
===================
I would have done this one, but you were too lazy to make it clear if you mean

or

=================
The other tutor spent his time assuming the former.
-----------
Making the problem clear is your responsibility.
|
|
|