Question 634796: Hi, I've been stuck on this one for a considerable amount of time.
=> Show that the equation 4cos(2x)-3sin(x)csc(x)^3+6 = 0, can be expressed as
8y^4-10y^2+3=0 if sin(x) = y
Hence, solve the equation for x
Thankyou for your help
Found 2 solutions by ewatrrr, jsmallt9:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
4cos(2x)-3sin(x)csc(x)^3+6 = 0
4cos(2x)-3/sin^2(x)+6 = 0
cos(2x)= 1-2sin^2x
4(1-2sin^2x) - (3/sin^2(x))+6 = 0 |Multiplying thru by sin^2x so as all denominators = 1
-8sin^4 + 4sin^2 - 3 + 6sin^2x = 0
8sin^4 + 10sin^2 - 3 = 0
8y^4-10y^2+3=0 if sin(x) = y
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
As the problem suggest, you want everything expressed in terms of sin(x). SO we will start by substituting for the 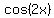 and and 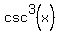 . The csc is easy. csc is the reciprocal of sin. So . The csc is easy. csc is the reciprocal of sin. So  . We have three variations for cos(2x):Since we want everything in terms of sin(x), we will use the third variation. Substituting in we get: . We have three variations for cos(2x):Since we want everything in terms of sin(x), we will use the third variation. Substituting in we get:

Note the use of parentheses! These are important when making substitutions. Simplifying we get:


Now that everything is in terms of sin(x), the next task is to get rid of the fraction. Multiplying both sides by  we get: we get:

As you may see, we're getting close. We can get the signs right if we multiply both sides by -1:

And rearrange the terms:

Now we can substitute "y" for "sin(x)":

The reason we made this substitution is that it is easier to see how to solve

than it is to see how to solve

(Eventually you will see how to solve without making the substitution.) Note: An even better substitution is  This would make the substituted equation: This would make the substituted equation:

which I think you would agree is even easier to solve than:

But we will go with the substitution your teacher/book suggested.

is an equation in what is called quadratic form. (A "pure" quadratic would have y-squared and y terms.) We can solve it with the same methods used to solve pure quadratics. One of these is factoring:

If this factoring is not immediately obvious to you, then look at it for a while and let it sink in. Multiply it back out and see if you get  . Look back at our alternate substitution, . Look back at our alternate substitution,  , and think about how that would factor. It might help you see how we got the factors above. , and think about how that would factor. It might help you see how we got the factors above.
Now we use the Zero Product Property:
 or or 
Solving these...
 or or 
 or or 
Finding the square root of each side (and not forgetting about the negative square roots) we get:
 or or  or or  or or 
Rationalizing the denominators...
 or or  or or  or or 
 or or  or or  or or 
 or or  or or  or or 
 or or  or or  or or 
We've solved for y. But we really want to solve for x. So it is time to substitute sin(x) back in for the y:
 or or  or or  or or 
All of these are special angle sin's so every x is a special angle (so put your calculator away).
We should recognize that the reference angle for both  or or  will be will be  . And since we have both positive and negative . And since we have both positive and negative  , x will terminate in all four quadrants. So for , x will terminate in all four quadrants. So for  or or  : :
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
with the middle two equations simplifying to:
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
For  and and  we should recognize that the reference angle will be we should recognize that the reference angle will be  and x will again terminate in all four quadrants (since we have both positive and negative and x will again terminate in all four quadrants (since we have both positive and negative 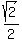 . This gives us: . This gives us:
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
with the middle two equations simplifying to:
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
The full general solution to your equation is all 8 of the equations above:
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
 (1st quadrant, (1st quadrant,  ) )
 (2nd quadrant, (2nd quadrant,  ) )
 (3rd quadrant, (3rd quadrant,  ) )
 (4th quadrant, (4th quadrant,  ) )
|
|
|