SOLUTION: can you help me find the inverse of the function g(x)= x/(x+2)

Algebra ->  Inverses -> SOLUTION: can you help me find the inverse of the function g(x)= x/(x+2)      Log On


   

Question 63476: can you help me find the inverse of the function g(x)= x/(x+2)
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Can you help me find the inverse of the
function g(x)= x/(x+2)

1. Replace g(x) by y

           y = x/(x+2)

2. Interchange x and y

           x = y/(y+2)

3. Solve for y:

           x = y/(y+2)

      x(y+2) = y

     xy + 2x = y

          2x = y - xy

          2x = y(1 - x)

(2x)/(1 - x) = y

           y = (2x)/(1 - x) 

4. Replace y by f-1(x)
      
      f-1(x) = (2x)/(1 - x)

To check, draw the graph of f(x)

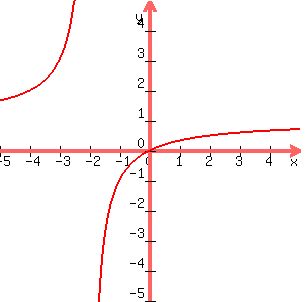+graph%28+300%2C+300%2C+-5%2C+5%2C+-5%2C+5%2Cx%2F%28x%2B2%29+%29+

On the same axis, draw the graph of f-1(x)

+graph%28+300%2C+300%2C+-5%2C+5%2C+-5%2C+5%2Cx%2F%28x%2B2%29%2C+2x%2F%281-x%29+%29+

Draw the indenty line, where y and x are identical, that
is, the line whose equation is y = x.

+graph%28+300%2C+300%2C+-5%2C+5%2C+-5%2C+5%2Cx%2F%28x%2B2%29%2C+2x%2F%281-x%29%2C+x+%29+

and we see that the original function and the inverse are
reflections of each other in the identity line, and form 
a symmetrical pattern. So the inverse is correct.

Edwin