|
Question 634592: what is square root of 50 + square root of 0.5 + 1 over the square root of 0.5 + sixth root of 8 + fourth root of 2500
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!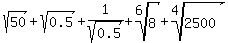 
None of these terms are like terms (yet). So we cannot (yet) add them together. All we can do right now is to simplify them. I'll do them one at a time.
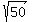
To simplify this we look for perfect square factors of the radicand. ("Radicand" is the name for the expression inside a radical.)
Then we use a property of radicals,  , to split the square root into two:
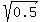
Finding perfect square factors of a decimal is not easy. So it is often easier to rewrite the decimal as a fraction:
and then simplify that. First we make the denominator a perfect square:
Then we use another property of radicals,  , to split the square root:
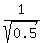
This is the reciprocal of the previous term. So we can use the previous result to help us with this one:
Now we just have to rationalize the denominator and simplify:
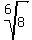
The direct way to simplify this is to find 6th power factors of 8. Unfortunately there are none. But we are not stuck. If the root type can be factored then the root can be expressed as a root of a root. In this case 6 can be factored into 2*3. So a sixth root is the same as a square root of a cube root (and vice versa). To see this more clearly we can use fractional exponents:
 or
Because 8 is a perfect cube,  , I am going to use the square root of a cube root version:
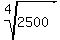
There are not power of 4 factors in 2500. But we can use a similar process as we just used with the 6th root. A 4th root, since 4 = 2*2, is the same as a square root of a square root:
Now we simplify the inner square root by finding perfect square factors:
We simplified 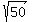earlier so we can re-use that result:
So our expression with the simplified radicals is:
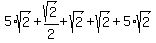
With all these square roots of 2, we now have some like terms to add. First, however, I'm going to rewrite the second term to make it easier to add to the other terms. Since dividing by 2 is the same as multiplying by 1/2 we can rewrite the second term as a multiplication:
Now we can add. Exactly like
|
|
|
| |
