Question 634548: I'm lost - I saw a math tutor today but he got side tracked and I'm just more confused. Here is the problem:
Solve the inequality log (base x) 5 < log (base 5) x
remember that x>0 and x≠1
rewrite each logarithm in terms of a common base, move both expressions to the same side of the inequality so that everything is being compared with zero. find a common denominator to combine the two expressions. Find the critical values of the combined expression, that is, find the values of x that make the numerator equal 0 and the values of x that make the denominator equal zero, find these values algebraically. I can muddle through some of this but I'm also required to detail out "why" I'm doing each step... I don't know how to describe the how and why in words.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 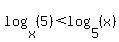
You are right in thinking we need a common base, either x or 5 or some third number. Using some third number will work but it makes things more complicated (as you will see shortly), so we will use a common base of x or 5. I'll use x. Using the base conversion formula,  to convert the base x log into an expression of base 5 logs: to convert the base x log into an expression of base 5 logs:
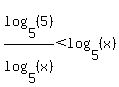
The numerator of the fraction is equal to 1 (since  ) so this will simplify. (This is why using x or 5 as the common base makes things simpler.): ) so this will simplify. (This is why using x or 5 as the common base makes things simpler.):

As you indicated we could continue by making one side zero, etc. And I will do this shortly. But this inequality can be solved much more easily if you look at what it is saying and if you understand certain things about how numbers work.
This equality says that some number, 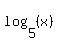 , is greater than its reciprocal (1/q is the reciprocal of q). When can a number be less than its reciprocal? If you understand reciprocals well you will know that , is greater than its reciprocal (1/q is the reciprocal of q). When can a number be less than its reciprocal? If you understand reciprocals well you will know that- If
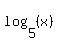 is positive (i.e. is positive (i.e. 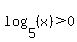 , then , then 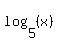 must be greater than 1. "Positive and greater than 1" translates into: must be greater than 1. "Positive and greater than 1" translates into:
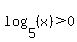 and and 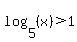
which simplifies to just:
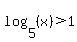 - If
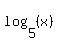 is negative (i.e. is negative (i.e. 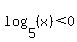 , then it works the opposite of the way it works for positives. We want , then it works the opposite of the way it works for positives. We want 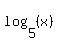 to be between 0 and -1. (Think about this and think about reciprocals. It should make sense.) "Negative and between 0 and -1" translates into: to be between 0 and -1. (Think about this and think about reciprocals. It should make sense.) "Negative and between 0 and -1" translates into:
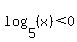 and and 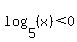 and and 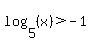
which simplifies to just:
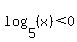 and and 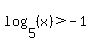
Since 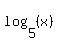 could be positive or negative, the full solution will come from: could be positive or negative, the full solution will come from:
(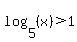 ) or ( ) or (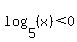 and and 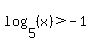 ) )
If this makes sense to you and if you think your teacher will accept this, then skip to "THE FINISH" below where I will finish this. Otherwise, keep reading. I will now solve this by getting one side to be zero, etc.

First let's get rid of the fraction. To do this we will multiply each side by 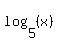 . But we have to careful doing this because this is an inequality, . But we have to careful doing this because this is an inequality, 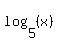 might be negative and if we multiply an inequality by a negative number we must reverse the inequality. To do this correctly we must generate two inequalities, one for when might be negative and if we multiply an inequality by a negative number we must reverse the inequality. To do this correctly we must generate two inequalities, one for when 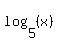 is positive (and we don't reverse the inequality) and one for when is positive (and we don't reverse the inequality) and one for when 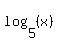 is negative (and we do reverse the inequality): is negative (and we do reverse the inequality):
(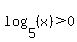 and and 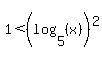 ) or ( ) or (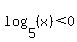 and and  ) )
Making the right side 2nd and 4th inequalities a zero:
(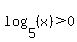 and and 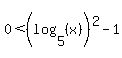 ) or ( ) or (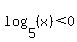 and and 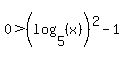 ) )
Factoring the 2nd and 4th inequalities (using the difference of squares pattern:  ): ):
(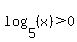 and and 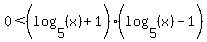 ) or ( ) or (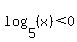 and and 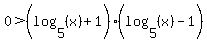 ) )
Next I will deal with this in parts. The first "half":
(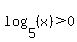 and and 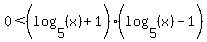 ) )
says that the log is positive and a product of two factors is greater than zero (IOW, positive). (Note: Always read inequalities form where the variable is. The variable in 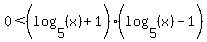 is on the right so we should read it from right to left. And from right to left, "<" is a "greater than".) And how does a product of two numbers become positive? Answer: If both numbers are positive or if both numbers are negative. And since is on the right so we should read it from right to left. And from right to left, "<" is a "greater than".) And how does a product of two numbers become positive? Answer: If both numbers are positive or if both numbers are negative. And since 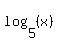 is positive, doesn't is positive, doesn't 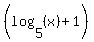 have to be positive, too? So we can't have two negative, jsut two positives And since we already know that have to be positive, too? So we can't have two negative, jsut two positives And since we already know that 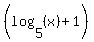 is positive, then we just have to say that is positive, then we just have to say that 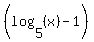 is positive, too. negative! So the first half simplifies to: is positive, too. negative! So the first half simplifies to:
(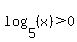 and and  ) )
Adding 1 to both sides of the second inequality we get:
(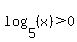 and and 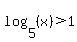 ) )
which simplifies to just:
(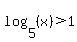 ) )
Next, let's look at the second "half":
(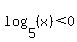 and and 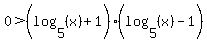 ) )
which says that the log is negative and a product of two numbers is negative. A product of two numbers is negative only when one is positive and the other is negative. Since the log is negative, the factor 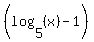 must be negative, too. So the must be negative, too. So the 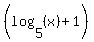 must be positive: must be positive:
(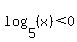 and and 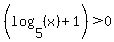 ) )
Subtracting 1 from both sides of the second inequality we get:
(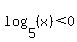 and and 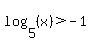 ) )
Putting our simplified "halves" back together we have:
(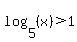 ) or ( ) or (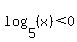 and and 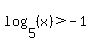 ) )
Note how this is exactly what we got using some logic and our understanding of reciprocals!
THE FINISH
Solving
(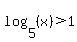 ) or ( ) or (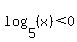 and and 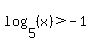 ) )
Rewriting each of these in exponential form:
(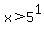 ) or ( ) or (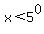 and and 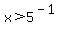 ) )
Simplifying:
(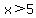 ) or ( ) or (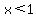 and and  ) )
This is our solution. Translated: x can be any number larger than 5 or any number between 1/5 and 1.
|
|
|