Question 634450: Find the exact value of sin((2x),cos(2x) given
tan(x)=-9/40, -pi/2 < x < 0
Please solve and explain.
Thanks
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Note: On a second look at this problem I realize that I made a mistake. Although the point (-9, 40), which I used in my initial solution, would have a tan of -9/40, that was not the right point to use. The point (9, -40) would also have the same tan. And because 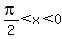 , the angle terminates in the 4th quadrant. This makes (9, -40) the right point to use. (The point (-9, 40) is in the 2nd quadrant.) Either way, the "r" still works out to be 41. I have corrected the answers below.
\We usually learn about ain's, cos's, etc. in terms of "opposite", "adjacent" and "hypotenuse". We can also learn them in terms of coordinates, x and y, and the distance from the origin, usually called "r":
sin(x) = opposite/hypotenuse = y/r
cos(x) = adjacent/hypotenuse = x/r
tan(x) = opposite/adjacent = y/x
csc(x) = 1/sin(x) = r/y
sec(x) = 1/cos(x) = r/x
cot(x) = 1/cot(x) = x/y
To see this clearly- Plot any point
- Draw the segment from the origin to this point. Label this segment as "r".
- Draw a vertical segment from the point to the nearest part of the x-axis. Label this segment as "y".
- Label the part of the x-axis between the origin and where the vertical segment hits the x-axis as "x"
- Look at the right triangle you have drawn. See if the ratios in terms of x, y and r make sense.
- Repeat with new points until you see the sense of the ratios above.
Now that we have the correct "x" and "y". All we need is the "r" value. For this we can use the Distance Formula for the distance between the origin and the point (9, -40):
Now we're ready to fill in our ratios:
sin(x) = opposite/hypotenuse = y/r = -40/41
cos(x) = adjacent/hypotenuse = x/r = 9/41
tan(x) = opposite/adjacent = y/x = 40/-9 = -9/40
csc(x) = 1/sin(x) = r/y = 41/-40 = -41/40
sec(x) = 1/cos(x) = r/x = 41/-9 = 9/41
cot(x) = 1/cot(x) = x/y = -40/9
|
|
|
