SOLUTION: The number of cell phone minutes used by high school seniors follows a normal distribution with a mean of 500 and a standard deviation of 50. 1.What is the probability that a st

Algebra ->  Probability-and-statistics -> SOLUTION: The number of cell phone minutes used by high school seniors follows a normal distribution with a mean of 500 and a standard deviation of 50. 1.What is the probability that a st      Log On


   

Question 634248: The number of cell phone minutes used by high school seniors follows a normal distribution with a mean of 500 and a standard deviation of 50.
1.What is the probability that a student uses fewer than 600 minutes?
2.What is the probability that a student uses fewer than 400 minutes?
3.What is the probability that a student uses more than 350 minutes?
4.What is the probability that a student uses more than 580 minutes?
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

mean of 500 and a standard deviation of 50. z = 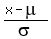%28x-mu%29%2Fsigma

P(x < 600)= P(z <  2)= .9773 or 97.73%  | using NORMSDIST Excel function to find P knowing z

P(x < 400)= P(z < -2)= .0228 or 2.28%

P(x > 350)= P(z > -3)= .9987 or 99.87%

P(x > 580)= P(z > 1.6) = .0548 or 5.48%



Important to Understand z -values as they relate to the Standard Normal curve:

Below:  z = 0, z = ± 1, z= ±2 , z= ±3 are plotted.  

Note: z = 0 (x value the mean) 50% of the area under the curve is to the left and 50%  to the right