Question 634132: solve 2sec^2 x +5tanx -3 = 0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Solving Trig equations like this one usually involves the following three stages:- Using algebra and/or Trig properties to transform the given equation into one or more equations of the form:
TrigFunction(expression) = number - Find the general solution for each of the equations from step 1. Since Trig functions are periodic, these general solution equations will express the infinite number of solutions to the equations from step 1.
- Often, but not always, the problem requests specific solutions like "find the smallest positive solution" or "find all solutions between
 and and 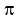 ". Use the general solution equations to find these specific solutions. ". Use the general solution equations to find these specific solutions.
Let's see this in action.
1. Transform the equation.
If you don't immediately see how to achieve the desired form, then some things to try are:- Use Trig properties to get all the arguments to match
- Use Trig properties to get all the functions to match. Sometimes this involves rewriting any tan, cot, sec or csc's into sin's and/or cos's.
The arguments are both x's so they already match. We do have two different functions, sec and tan, and fortunately there is a property that connects them directly:  . So by using this property we can replace the sec squared and get an equation with only tan's: . So by using this property we can replace the sec squared and get an equation with only tan's:

Note the use of parentheses. This is very important when making substitutions of multiple-term expressions. In this case the parentheses tell us to use the Distributive property to multiply by the 2:

Combining the 2 and the -3:

This is a quadratic equation in terms of tan(x). Unfortunately it does not factor. (Did you post the problem correctly? Usually these problems factor at this point.) So we must use the Quadratic Formula:

which simplifies as follows:




which is short for:
 or or 
These equations in the desired form and they are exact expressions for tan(x). But they are not special angle values for tan (like 0, 1,  , etc.) so we will need decimals to proceed: , etc.) so we will need decimals to proceed:
 or or 
 or or 
 or or 
2. General solution.
We are looking to express all the angles whose tan is either 0.18614066 or -2.68614066. We'll do them one at a time.
tan(x) = 0.18614066
Using the inverse tan button, "tan^-1", on 0.18614066 we should get a reference angle of 0.18403446 radians. Since this tan is positive we know that x terminates in either the 1st or 3rd quadrants. This, combined with the reference angle gives us:
 for the 1st quadrant angles; and for the 1st quadrant angles; and
 for the 3rd quadrant angles. for the 3rd quadrant angles.
Repeating this process for:
tan(x) = -2.68614066
Using the inverse tan button, "tan^-1", on 2.68614066 we should get a reference angle of 1.21441128 radians. (Note: When looking for reference angles, like we are here, do not enter negative numbers into the inverse functions! This is why we used 2.68614066 and not -2.68614066.) Since this tan is negative we know that x terminates in either the 2nd or 4th quadrants. This, combined with the reference angle gives us:
 for the 2nd quadrant; and for the 2nd quadrant; and
 for the 4th quadrant for the 4th quadrant
The full general solution is all four of these equations:
 or or
 or or
 or or

3. Specific solution.
Your problem did not ask for a specific solution. Your answer, then, is the general solution equations above.
If your problem had asked for specific solutions then you would find these by trying various integer values for n in each of the general solution equations until you're convinced that no other specific solutions are to be found.
Notes on the general solution:- The part before "+
 " specifies a single angle (in this case a single angle with the right tan value). " specifies a single angle (in this case a single angle with the right tan value). - The "n" in these equations can be replaced by any and all integers. Each integer value for n will result in a different value for x. All of these x's are solutions.
- The "+
 " part of these equations is how we say "and any co-terminal angle". " part of these equations is how we say "and any co-terminal angle". - For the 4th quadrant we could have used
 instead. instead.
|
|
|