|
Question 633554: Find an equation of the parabola that satisfies the given conditions.
Focus F(9, 9), directrix y = -5
( )^(2)=28( )
Found 2 solutions by ewatrrr, Edwin McCravy:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi,
Parabola: Focus F(9, 9), directrix y = -5 V(9,2) p = 7
(x-9)^2 = 28(y-2)
the vertex form of a Parabola opening up(a>0) or down(a<0), 
where(h,k) is the vertex and x = h is the Line of Symmetry
The standard form is  , where the focus is (h,k + p)
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
The lady above mentioned the form of the parabola that is used when studying
quadratic functions, y=a(x-h)²+k, when you are not concerned with the
focus or the directrix. The form to use when you are studying
conic sections is the other one she gave. When studying conic sections you
use these two forms:
(x-h)² = 4p(y-k) and (y-k)² = 4p(x-h)
where |p| is the distance between the vertex and the focus,
and (h,k) is the vertex.
The first one is for parabolas opening upward or downward.
If p is positive the parabola opens upward, and if negative
it opens downward.
The second one is for parabolas opening rightward or leftward.
If p is positive the parabola opens rightward, and if negative
it opens leftward.
First we will plot the focus F(9,9) and draw the directrix,
which is the line with the equation y=-5, which is a horizontal
line 5 units below the x-axis, drawn in green below:
The vertex is a point half-way between the focus and the directrix.
So we draw a line from the focus directly down to the directrix. I'll
draw that one in blue.
The midpoint of that blue line is the vertex of the parabola. We know
that its x-coordinate is the same as the x-coordinate of the focus, 9.
We can find its y coordinate by averaging the y coordinate of the focus,
9 and the y-coordinate of all points on the directrix, -5, averaging
them is  . So the vertex is V(9,2)
Now draw a square which has its left side as the blue line
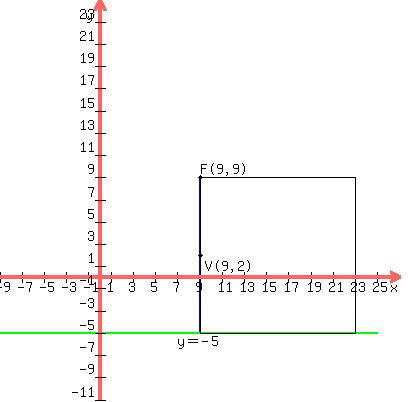Now draw a square which has its right side as the blue line
Now we can sketch in the parabola with its vertex and passing through the
the corners of those two squares.
There are 7 units between the vertex and the focus, so p = 7, positive
because the parabola opens upward. The vertex is (h,k).
So the equation of the parabola is of the form:
(x-h)² = 4p(y-k)
whete (h,k) = (9,2) and p = 7
Substituting
(x-9)² = 4(7)(y-2)
(x-9)² = 28(y-2)
BTW, you did not have to to be given the value of 4p which is 28.
Edwin
|
|
|
| |
