|
Question 633025: Ryan buys a computer system for $3800. For tax purposes, he declares a linear depreciation (loss of value) of $400 per year. Let “y” be the declared value of the computer after “x” years.
What is the slope of the line that models this depreciation?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The declared value (in $) is  for for  . .
After  years, the declared value has decreased by $ years, the declared value has decreased by $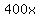 to to
 or in a more conventional linear equation in slope-intercept form or in a more conventional linear equation in slope-intercept form

The slope intercept form of a linear equation looks like
 , ,
with a number  called the slope, multiplied to the variable called the slope, multiplied to the variable  , ,
and a number  called the y-intercept, called the y-intercept,
added to that product to yield  . .
In this case the slope is  . .
When the slope is negative, as in this case, we know that  decreases as decreases as  increases. increases.
The number  is called the slope because it measures how fast is called the slope because it measures how fast  increases or decreases for an increase of one unit in increases or decreases for an increase of one unit in  , increasing for positive slopes, and decreasing for negative slopes. , increasing for positive slopes, and decreasing for negative slopes.
For  , ,  , and if we add , and if we add  to the to the  , ,
we find that for  , ,  has increased by has increased by 
|
|
|
| |