Question 632824: An airplane diving at an angle of 40.9 degrees below the horizontal drops a mailbag from an altitude of 900m. the bag strikes the ground 5.00s after its released.
a) what us the speed of the plane?
b) how far does the bag travel horizontally during its fall?
c) what are the horizontal and vertical components of its velocity just before it strikes the ground?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! DEFINITIONS, EXPLANATIONS, SET-UP:
Let t be the time, in seconds, counted from the time the mailbag is dropped.
Let x be the speed of the plane (the magnitude of its velocity).
It can be thought of as the sum of a horizontal velocity component and a vertical velocity component (we will deal with the magnitude of those components as a number/speed, taking them positive when in the direction the plane was moving).
The mailbag has the velocity as the plane at the time it is released.
For the mailbag, after release, the horizontal (positive) speed does not change,
while the vertical speed (positive, downwards) increases due to the acceleration of gravity. (Air resistance is always considered negligible in this type of problems).
As the bag hits the ground, it is still directly below the airplane (if the airplane velocity has not changed), because the horizontal component of the velocities of plane and bag are still the same.
a) The vertical downwards speed of the plane (in m/s) is
 (rounding  )
The bag accelerates downwards at  
The bag's VERTICAL (downwards) SPEED is
 , increasing linearly as the bag falls,
going from  to 
The average downwards speed is 
and over 5 seconds it will cover a distance (in meters) of
 equal to the 900 m altitude of the plane at bag release. So,
 -->  -->  -->  -->  -->  m/s (rounded)
ALTERNATE calculation explanation:
 or  takes you to the same equation.
b) The horizontal distance covered by the bag (and presumably the plane) while the bag was falling is the constant horizontal velocity times the 5 seconds of time elapsed.
The horizontal speed component of the bag (and plane) velocity is
 (rounding  )
Substituting the plane speed as  (in m/s, rounded),
the horizontal speed is  m/s
Over the 5 seconds it was falling, the bag traveled horizontally
(206 m/s)(5 s) =   .
c) The horizontal component of the bag velocity is assumed to be the same on the plane and throughout the fall, and was found above as   .
The vertical component was found above (far above) to have reached its maximum of
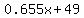 after 5 seconds of fall (as the bag hit the ground).
Substituting the plane velocity found in the first part,
that vertical component is  m/s.
|
|
|
