Question 632353: If you wrap a piece of wire 8 times around a pipe and the length of the pipe is 20cm and the circumference is 6cm, what is the length of the wire?
Found 2 solutions by rapaljer, Alan3354:
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! When I first read this problem, I'm afraid that I interpreted incorrectly. This is actually supposed to be a wire wrapped AROUND and UP the pipe in a spiral manner (this is called a HELIX in case you want to look into this for additional explanation),
Begin by picturing a vine or a wire wrapped 6 times around a tree trunk that is 20 feet high and whose circumference is 8 feet. If the circumference is 8 feet, then the DIAMETER of the trunk of the tree is 8/pi. Now, suppose you cut the tree off at the base, and lay the tree flat on the ground, and UNWRAP the vine or wire by fastening the vine at the top of the tree and rolling the tree on the ground. When the vine is completely unwrapped, the vine will form the hypotenuse of a right triangle, where the first leg (the height of the triangle!) is the original position of the tree on the ground, which is 20 feet, and the second leg (the base of the triangle!) is the path traced out by the base of tree as it was rolled to unwind the vine. Can you picture this?
The tricky part to figure is the length of the second leg of the right triangle. Each time you rolled the tree to unwrap one complete wrapping of the vine, the tree rolls ONE circumference, which would be 8 feet. Since the vine wrapped a total of 6 times around the tree, this means that the total distance the tree rolls to completely unwrap the vine will be 6*8 feet or 48 feet.
So, picture a right triangle whose height is 20 feet and whose base is 48 feet. The total length of the vine is the hypotenuse, which is 
Of course, change the feet to cm for this particular problem. The final answer is 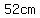 . .
Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you wrap a piece of wire 8 times around a pipe and the length of the pipe is 20cm and the circumference is 6cm, what is the length of the wire?
--------------
If you mean the wire is wrapped in a helical manner along the length of the pipe, then:
If you unwrap it on a flat surface, you get a right triangle. The base is 8 turns of the pipe = 8*6 = 48 cm
The other leg is the length of the pipe = 20 cm
The length of the wire is the hypotenuse

w = 52 cm
|
|
|