|
Question 63222: I have many word problems to solve that are similar to this one, but I need help with the questions on this one word problem so I can use it as an example to look at and answer the other problems on my own. Here is the word problem and questions below......... In most businesses, increasing prices of their product can have a negative effect on the number of customers of the business. A bus company in a small town has an average number of riders of 1,000 per day. The bus company charges $2.00 for a ride. They conducted a survey of their customers and found that they will lose approximately 50 customers per day for each $.25 increase in fare.
Given the description above, graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), find the slope of the graph, find the price at which there will be no more riders, and find the maximum number of riders possible. The vertical axis is the number of riders per day, and the horizontal axis is the fare.
What is the graph and graph type?
What is the slope of the graph?
1)The bus company has determined that even if they set the price very low, there is a maximum number of riders permitted each day. If the price is $0 (free), how many riders are permitted each day?
2)If the bus company sets the price too high, no one will be willing to ride the bus. Beginning at what ticket price will no one be willing to ride the bus?
3) It is approximately 300 miles from Chicago, Illinois, to St. Louis, Missouri. Allowing for various traffic conditions, a driver can average approximately 60 miles per hour.
a)How far have you traveled after 3 hours?
b)How far have you traveled after 4 hours?
c)How far have you traveled after t hours? i.e. write a linear function that expresses the distance traveled, d, as a function of time, t.
d)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled 3 hours?
e)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled 4 hours?
f)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled t hours? i.e. write a linear function that expresses the distance to be traveled to reach St. Louis, s, as a function of time, t.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bus company in a small town has an average number of riders of 1,000 per day. The bus company charges $2.00 for a ride. They conducted a survey of their customers and found that they will lose approximately 50 customers per day for each $.25 increase in fare.
Given the description above, graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), find the slope of the graph, find the price at which there will be no more riders, and find the maximum number of riders possible. The vertical axis is the number of riders per day, and the horizontal axis is the fare.
:
Let x = cost per ride. Let y = number of customers
Given x1 = 2; y1 = 1000; x2 = 2.25; y2 = 950
:
Find the slope: m = (y2-y2)/(x2-x1)
m = 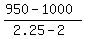 = = 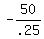 = -200 is the slope (m) = -200 is the slope (m)
:
Find the equation using the point/slope equation: y -y1 = m(x - x1)
y - 1000 = -200(x - 2)
y - 1000 = -200x + 400
y = -200x + 400 + 1000
y = -200x + 1400
What is the graph and graph type?
I assume you know how to plot this graph from the equation y = -200x + 1400
:
This is the graph and it is linear (a straight line)

:
What is the slope of the graph?
We calculated the slope m = -200
:
:
1)The bus company has determined that even if they set the price very low, there is a maximum number of riders permitted each day. If the price is $0 (free), how many riders are permitted each day?
:
You can see by the graph and the equation that if it was free (x=0) there
would be 1400 riders
:
:
2)If the bus company sets the price too high, no one will be willing to ride the bus. Beginning at what ticket price will no one be willing to ride the bus?
:
This occurs when y = 0, (x intercept occurs at $7.00 as you can see by the graph)
Also if you substitute 7 for x in the equation you would get y = -200(7) + 1400
:
:
:
3) It is approximately 300 miles from Chicago, Illinois, to St. Louis, Missouri. Allowing for various traffic conditions, a driver can average approximately 60 miles per hour.
:
a)How far have you traveled after 3 hours? 3*60 = 180 mi
b)How far have you traveled after 4 hours? 4*60 = 240 mi
c)How far have you traveled after t hours? 60t
i.e. write a linear function that expresses the distance traveled, d, as a function of time, t.
Let x = time: y = dist: x1 = 3, y1 = 180, x2 = 4, y2 = 240
Find the slope: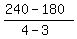 = = 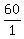 = +60 is the slope (m) = +60 is the slope (m)
:
Find the equation: y - 180 = 60(x - 3)
y - 180 = 60x - 180
y = 60x -180 + 180
y = 60x
:
Graph y = 60x
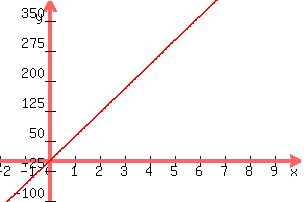
;
:
d)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled 3 hours?
e)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled 4 hours?
f)How far will you HAVE LEFT to travel to reach St. Louis after you have traveled t hours? i.e. write a linear function that expresses the distance to be traveled to reach St. Louis, s, as a function of time, t.
:
See if you can figure out this using the method we used above:
1.Determine the x,y coordinates from above questions
2.Find the slope (m)
3.Find the equation using the point/slope formula
4.plot the Graph
:
the equation will be y = -60x + 300 and the graph will look like this:

:
Let me know how you do.
|
|
|
| |