Hi,
three consecutive odd positive integers  ,
, 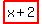 ,
, 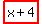
2 times the sum of all three is 9 less than the product of the first and second integers
2(3x + 6)=x(x+2)-9
6x + 12 = x^2 + 2x-9
0 = x^2-4x - 21
0 = (x-7)(x+3) x = 7
The three consecutive odd positive integers are 7 , 9 , 11
and...
