Question 631734: Please help me solve this problem:
The length of a rectangle is 7 cm more than its width. If the length is increased by 2 cm and the width increased by 4 cm, the area will be increased by 54 cm^2. Find the original length and width of the rectangle.
Thank you so much!
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Please help me solve this problem:
The length of a rectangle is 7 cm more than its width. If the length is increased by 2 cm and the width increased by 4 cm, the area will be increased by 54 cm^2. Find the original length and width of the rectangle.
Thank you so much!
Let original width of rectangle be W
Then original length = W + 7
Increasing length by 2 makes it W + 7 + 2, or (W + 9) cm
Increasing width by 4 makes it (W + 4) cm
Original area = LW, or W(W + 7), or 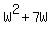
Adjusted area = LW, or (W + 9)(W + 4), or 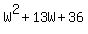
Since adjusted area is increased by  , then: , then:


13W - 7W = 20
6W = 20
W, or original width = 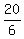 , or , or  , or , or  cm cm
Original length = W + 7, or 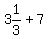 , or , or 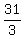 , or , or 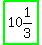 cm cm
You should be able to do the check!!
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|