Question 631238: how can i solve log[base8](x+5)-log[base8](x-2)=1?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!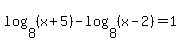 
Solving equations like this usually starts with using algebra and/or properties of logarithms to transform the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
Since your equation has a "non-log" term of 1, it will be harder for us to reach the second, "all-log" form. So we will aim fir the first form.
The first form has just one, isolated log. Our equation has two logs. Somehow we need to find a way to eliminate one log or to combine the two logs into one. To eliminate a log we- have it cancel out with another log; or
- we replace it with a number if it is a well-known log. For example, if we had log(100), then we could replace this with a 2 since it is well-known that
 making log(100) = 2.
Neither of these are available to us in this problem.
To combine logs, you- Add or subtract them if they are like terms. (Like logarithmic terms have the same bases and same arguments.); or
- Use one of the following properties:These properties require logs with the same bases and coefficients of 1.
Our two logs are not like terms so we cannot subtract them. But they do have the same bases and they do have coefficients of 1. So we can use the properties to combine them. We will use the second property because its logs, like ours, have a "-" between them:
We now have the desired form.
The next step with the first form is to rewrite the equation in exponential form. In general,  is equivalent to  . Using this pattern on our equation we get:
which simplifies to:
Now that the logs are gone, we can solve this equation with plain algebra. Let's start by eliminating the fraction nby multiplying both sides by (x-2):
which simplifies to:
Subtracting x from each side:
Adding 16:
Dividing by 7:
Last of all we check our solution(s). With these kinds of equations, checking is not optional! You must at least check to see that all arguments of all logarithms remain positive. If a "solution" makes an argument of a log zero or negative, that solution must be rejected/discarded because arguments to logs can never be zero or negative.
Use the original equation to check:
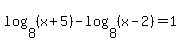
Checking x = 3:
We can already see that both arguments will turn out positive when x = 3. So this solution checks out. (If it had not checked out, then we would have to reject this solution. And since it was the only "solution" we found we would end up with no solution. IOW, the equation was impossible to begin with.)
|
|
|
