SOLUTION: Two lines bisect consecutive angles of a regular heptagon and and intersect in the heptagon's interior. Find the measure of the angle between the intersecting lines.

Given: OB bisects ∠ABC
       OC bisects ∠BCD

To find: the measure of ∠BOC

[Note: if you had proved that OB and OC intersect at the center, you
could just observe that ∠BOC is a central angle and has measure .  
But we will assume you haven't proved that.]  

The sum of the measures of the interior angles of an n-sided polygon
is given by the formula (n-2)×180°

Since this is a heptagon, n=7 and the sum of the measures of the 
interior angles is (7-2)×180° = (5)×180° = 900°

Since this heptagon is regular, all the interior angles are congruent
and have equal measure.  Therefore

m∠ABC = m∠BCD = 

Since OB and OC bisect those interior angles,

m∠OBC = m∠OCB = × = 

Since the sum of the measures of the interior angles of ᐃBOC is 180°,

m∠OBC + m∠OCB + m∠BOC = 180°
 +  + m∠BOC = 180°

                  + m∠BOC = 180°

                                  m∠BOC = 180° - 

                                  m∠BOC =  - 
                                  
                                  m∠BOC =  = °

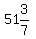Edwin