|
Question 630285: may you please help me reduce this rational expression into lowest terms
6x^5 - 48x^2/12x^3 + 24x^2 + 48x
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, please put parentheses around multiple term numerators and denominators. What you posted means:
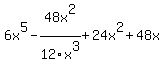
which I'm pretty sure is not the right expression. Making your expressions clear and not making the tutors try to figure out what you mean will result in faster responses.
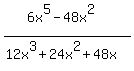
Reducing fractions is, as it's always been, a matter of finding and canceling any factors that are common to the numerator and denominator. So we start by figuring out what the factors are.
We'll start by factoring the numerator:
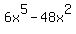
When factoring, always start by factoring out the greatest common factor (GCF), unless it is a 1 which is rarely factored out. The GCF here is 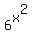 : :
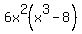
After the GCF, there are a variety of factoring techniques one can try. One of the methods is factoring by patterns and one of these patterns is:

The factor 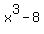 fits that pattern because fits that pattern because  is clearly a perfect cube and, since is clearly a perfect cube and, since  , so is 8. Using this pattern with an "a" of "x" and a "b" of "2" we get: , so is 8. Using this pattern with an "a" of "x" and a "b" of "2" we get:
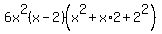
which simplifies to

None of these factors will factor any further so we are finished factoring the numerator. For reasons you'll see later, I'm going to rewrite 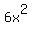 as 6*x*x: as 6*x*x:
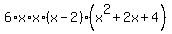
Now we'll factor the denominator:
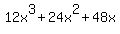
First the GCF of 12x:
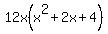
None of these factors will factor further. Again for reasons you'll see shortly, I'm going to rewrite 12x as 6*2*x:
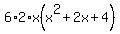
Now let's rewrite the fraction with the factored numerator and denominator:
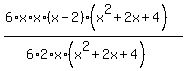
Looking at this you should be able to see some factors that are common to the numerator and denominator (and see why I rewrote 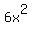 and 12x). These common factor can be canceled: and 12x). These common factor can be canceled:
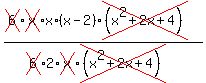
leaving:
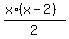
(Note: The 2's do not cancel! Only factors can be canceled and the 2 in the numerator is not a factor.) This may be an acceptable answer. Or you could multiply out the numerator:
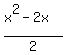
|
|
|
| |