|
Question 630069: find an nth degree polynomial function with the real coefficients satifying the given conditions n=4; i and 5i are zeros; f(-1)=104
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! To start we need all the zeros of the polynomial. A 4th degree polynomial will have 4 zeros.
We were given only two zeros. So the other two are "missing". To find these missing zeros, you have to know that if a polynomials with real coefficients as a complex zero, then the complex conjugate of that zero will also be a zero.
The standard form for a complex number is:
a + bi
The complex conjugate of this would be:
a - bi or a + (-bi)
The two zeros we've been given are complex (because of the "i"). So the complex conjugates of each of them will also be zeros of the polynomial. The zero, i, in standard form is:
0 + i
Its complex conjugate would be
0 - i or just -i
The zero 5i in standard form would be:
0 + 5i
Its complex conjugate would be
0 - 5i or just -5i
We now have all 4 zeros: i, -i, 5i and -5i. The next step is to write the polynomial in factored form. The factored form will include a factor for each zero and an optional constant factor. The factors for each zero will be of the form (x - z) where z is a zero. So our polynomial in factored form is:
f(x) = c(x - i)(x - (-i))(x - 5i)(x - (-5i))
where "c" is the optional constant factor that we have not yet found. This simplifies to:
f(x) = c(x - i)(x + i)(x - 5i)(x + 5i)
We will find the value for "c" last. The next step is to multiply out the factors with the zeros. This is actually fairly simple if- You multiply each pair of factors with conjugates first. Specifically, multiply (x-i)(x+1) first, then (x-5i)(x+5i) next, then multiply the results of these two multiplications.
- Use the
 pattern to multiply the conjugates quickly
Let's see this. First (x-1)(x+i) using the pattern:
Next ((x-5i)(x+5i) using the pattern:
Simplifying...
Since  :
Note how the i's are gone! This and being able to use the pattern are why we start the multiplications with the conjugates. Now we continue with the last multiplication, using FOIL:
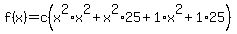
Simplifying...
As long as "c" is not zero, this polynomial will have the desired zeros. TO find the value for "c" we use the other given fact: f(-1) = 104:
Simplifying...
Dividing by 52:
So
Distributing the 2 we get:
|
|
|
| |
