|
Question 629914: two function f and g are defined by :
f(x)=2x+1
g(x)=x^2
verify that (fog)^-1 = g^-1 o f^-1
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Inverses of of functions are found by swapping the x's and y's. To perform this swap, I like to temporarily replace the function notation with a "y":
f(x) = 2x+1
y = 2x + 1
Swap the x's and y's:
x = 2y + 1 <=== This is the inverse, but not in a desired form
Solve for y:
x - 1 = 2y
Divide by 2 (or multiply by 1/2):
Doing the same for g(x):
+
Note: Because of the +, the inverse of g is not a function (i.e. some, in fact all, x's have more than one y value). And since this inverse is not a function, I do not believe it is proper to use function notation, g^-1 on it.
For the compositions it helps if we have a good understanding of what the function's definition is telling you. For example
f(x) = 2x+1
The left side tells us that the input to the function, between the parentheses after the function name, is being called "x". "x" is just a placeholder. It is just being used as a name for the input to the function. We could use any letter here to name the input. f(q) = 2q+1 is the exact same function as f(x)!!
The right side tells us what function f does with its input. It multiplies the input, x, by 2 and then adds 1. Since "x" is just a place holder, function f will take any input, multiply it by 2 and then add 1:
f(7) = 2(7) + 1
f(1002.4) = 2(1002.4) + 1
f(12x-3) = 2(12x-3) + 1
etc.
(fog)(x) is just another way to write f(g(x)). In f's parentheses we have "g(x)". So "g(x)" is the input to f. And what does f do to its input? Answer: it multiplies by 2 and then adds 1!:
f(g(x)) = 2(g(x)) + 1
Since we can substitute this in for g(x):
Now we find the inverse of fog:
+
Again, we get an inverse that is not a function.
For g^-1 o f^-1, we use the two inverses we found back at the start and feed the inverse of f into the inverse of g as its input: From the inverse of g, +, we can see that it finds the positive and negative square roots of its input. So it will do the same to f^1,  :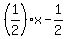
+
which matches the inverse of fog!
|
|
|
| |
