|
Question 629886: Solve
r(r-8)/(2r+6)<0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 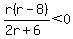
There are other ways to solve this but I'm going to try to show you what I consider to be the fastest, easiest way.
For reasons I will explain later, I am going to start by factoring out 2 in the denominator:
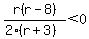
And then multiply both sides by 2:
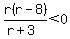
The keys to solving this are:- Recognizing that "less than zero" means the same thing as "negative". So this inequality says something is negative.
- The left side is the product of two numbers, r and r-8, divided by a third number, r+3. And how do you get a negative result when you have three numbers being multiplied and divided? With some thought I hope you can understand that you get a negative result when you have an odd number of negatives being multiplied and divided. With our three numbers (r, r-8 and 2r+6), we will need either one or three of them to be negative.
So to solve this problem we will translate "one factor is negative (and the others positive) or all three factors are negative" into a mathematical expression and then solve that expression.
The easier translation is "all three are negative":
(r < 0 and r-8 < 0 and r+3 < 0)
For "one is negative and the others positive", the straightforward approach is to express all three combinations:
((r < 0 and r-8 > 0 and r+3 > 0) or (r > 0 and r-8 < 0 and r+3 > 0) or (r > 0 and r-8 > 0 and r+3 < 0))
Together "one factor is negative (and the others positive) or all three factors are negative" translates into:
(r < 0 and r-8 < 0 and r+3 < 0) or ((r < 0 and r-8 > 0 and r+3 > 0) or (r > 0 and r-8 < 0 and r+3 > 0) or (r > 0 and r-8 > 0 and r+3 < 0))
From here we could go ahead and solve this. But I'm going to show you how to make this easier. If you don't understand any of the following, then go ahead and solve the above.
We can greatly simplify the above expression by using some simple logic. First, let's look at the three numbers involved. With some thought it should be clear that no matter what number "r" happens to be:
"r+3" will be larger than the other two
"r" will be next largest and
"r-8" will be the smallest of the three.
We can use this to our advantage. For example, if we want all three numbers to be negative, isn't it enough to know that the largest number is negative. If the largest is negative, won't the other two (smaller) number also have to be negative? So for "all three are negative" all we really need is:
r+3 < 0
We can use similar logic to simplify the expression for "one is negative and the others positive". If only one number is to be negative, doesn't it have to be the smallest number, r-8? And for the other two to be positive, doesn't the smaller of the two, have to be positive? So for "one is negative and the others positive" all we really need is:
(r-8 < 0 and r > 0).
So we can replace
((r < 0 and r-8 > 0 and r+3 > 0) or (r > 0 and r-8 < 0 and r+3 > 0) or (r > 0 and r-8 > 0 and r+3 < 0))
with
(r+3 < 0) or (r-8 < 0 and r > 0)
Either one can be solved and they will eventually give the same solution. But I think you'll agree that the simplicity and ease of solving the second expression is worth the extra thought. I'm only going to solve the simpler one:
(r < -3) or (r < 8 and r > 0)
One step and we're finished!
P.S. The reason I eliminated the factor of 2 way back at the beginning was that if the three numbers were r, r-8 and 2r+6, then we could not clearly know which factor was largest, which was smallest and which was in between. And then we could not use the simpler expressions to make it easy.
|
|
|
| |