SOLUTION: A small company produces both doll houses and sets of doll furniture. The doll houses take 3 hours of labor to produce, and the furniture sets take 8 hours. The labor available i

A small company produces both doll houses and sets of doll furniture. The
doll houses take 3 hours of labor to produce, and the furniture sets take 8
hours. The labor available is limited to 400 hours per week, and the total
production capacity is 100 items per week. Existing orders requare that at
least 20 doll houses and 10 sets of furniture be produced per week. Write a
system of inequalities representing this situation, where x is the number of
doll houses and y is the number of furniture sets. Then graph the system of
inequalities.

First we construct the labor hours inequality:

At 3 hours of labor for each of the x doll 
houses amounts to 3x hours of labor to make the 
x doll houses

At 8 hours of labor for each of the y furniture 
sets amounts to 8y hours of labor to make the y 
furniture sets.

So the total amount of labor is the sum of those, 
or 3x + 8y hours of labor

We are told that we are limited to 400 hours of 
labor so we write the labor hours inequality:

          3x + 8y < 400

Next we construct the items inequality:

The x doll houses amounts to x items per week

The y furniture sets amounts to y items per 
week.

So the total amount of items is the sum of 
those, or x + y items

We are told that we are limited to 100 items 
per week so we write the item inequality:

          x + y < 100

Next we construct the doll house inequality:

We are told that we must make at least 20 doll 
houses per week, so we write the doll house 
inequality:

          x > 20

Next we construct the furniture set inequality:

We are told that we must make at least 10 
furniture sets per week, so we write the 
furniture set inequality:

          y > 10

Now there are two obvious inequalities which 
tell us that the number of doll houses and the 
number of furniture sets must not be a negative 
number, so they are these:

         x > 0
         y > 0
  
So the six inequalities are

          3x + 8y < 400
            x + y < 100
                x > 20
                y > 10
                x > 0
                y > 0

We draw the boundary lines, which are
formed by replacing the inequality
symbols by = signs, so we have these
four boundary lines, and their intercepts:

                 3x + 8y = 400  (0,50),  (33.3,0)
                   x + y = 100  (0,100), (100,0) 
                       x = 20   (20,0) vertical line
                       y = 10   (0,10) horizontal line
                       x = 0    y-axis 
                       y = 0    x-axis

Since x and y are non-negative we draw only the upper
right quadrant, right of the y axis and above the x-axis:

Drawing the first boundary line in red:
            
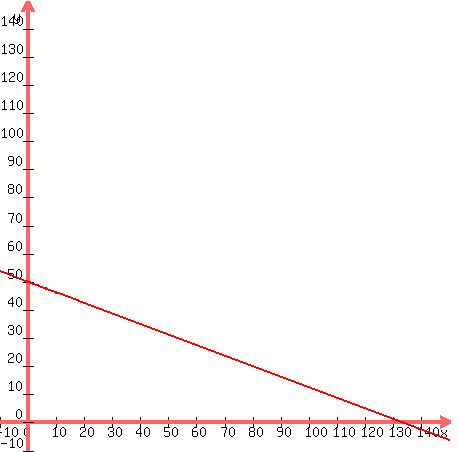Now since the origin (0,0) when substituted into the 
inequality 3x + 8y < 400 gives a true result
0 < 400 the graph is underneath this line because 
that is the side of that line that the origin is on.

Now we draw the second boundary line in green:
            
Now since the origin (0,0) when substituted into the 
inequality x + y < 100 gives a true result
0 < 100 the graph is underneath this line because 
that is the side of that line that the origin is on.

Now we draw the third boundary line in blue:
            
Now since the origin (0,0) when substituted into the 
inequality x < 20 gives a FALSE result
0 > 20 the graph is to the right of this blue
vertical line because that is the side the origin is
NOT on.

Now we draw the fourth boundary line in purple:
            
Now since the origin (0,0) when substituted into the 
inequality y > 10 gives a FALSE result
0 > 10 the graph is above this purple
horizontal line because that is the side the 
origin is NOT on.

We do not have to graph the last two boundary lines,
because they are the two axes, and we know that the
region to shade is always above the x-axis and to the
right of the y-axis.

So the area to be shaded is the region which is:
1. below the red slanted line
2. below the green slanted line
3. right of the blue vertical line
4. above the purple horizontal line

I can't shade that region on here, but you can on your 
paper. It's the 4-sided figure whose top side is red,
bottom side purple, left side blue, and right side 
green.


Edwin