sin[sin-1( ) + cos-1(x)] = 1
Let a = sin-1(
) + cos-1(x)] = 1
Let a = sin-1( ) and b = cos-1(x)
Then sin(a) =
) and b = cos-1(x)
Then sin(a) =  and cos(b) = x
And now our equation is
sin(a + b) = 1
Using an identity on the left side,
sin(a)cos(b) + cos(a)sin(b) = 1
Draw two right triangles, one with acute angle a and one with acute angle b:
and cos(b) = x
And now our equation is
sin(a + b) = 1
Using an identity on the left side,
sin(a)cos(b) + cos(a)sin(b) = 1
Draw two right triangles, one with acute angle a and one with acute angle b:

 Since the sine of a is
Since the sine of a is  and since
and since  , put
the numerator of
, put
the numerator of  , which is 1, on the side opposite a and
the denominator of
, which is 1, on the side opposite a and
the denominator of  which is 5, on the hypotenuse.
Since the cosine of b is x, we consider that as the fraction
which is 5, on the hypotenuse.
Since the cosine of b is x, we consider that as the fraction 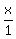 and since
and since  , put the numerator of
, put the numerator of 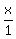 , which is x,
on the side adjacent b and the denominator of
, which is x,
on the side adjacent b and the denominator of 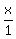 which is 1, on the
hypotenuse.
which is 1, on the
hypotenuse.
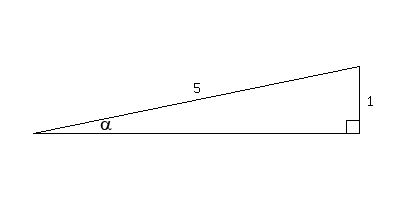
 Next we use the Pythagorean theorem to find the side adjacent a, and
the side opposite b:
a² + b² = c² a² + b² = c²
a² + 1² = 5² x² + b² = 1²
a² + 1 = 25 x² + b² = 1
a² = 24 b² = 1 - x²
a =
Next we use the Pythagorean theorem to find the side adjacent a, and
the side opposite b:
a² + b² = c² a² + b² = c²
a² + 1² = 5² x² + b² = 1²
a² + 1 = 25 x² + b² = 1
a² = 24 b² = 1 - x²
a =  b =
b = 

 Now we can use the right triangles above and their sides to substitute
into the equation:
sin(a)cos(b) + cos(a)sin(b) = 1
(
Now we can use the right triangles above and their sides to substitute
into the equation:
sin(a)cos(b) + cos(a)sin(b) = 1
( )(
)(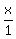 ) + (
) + (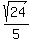 )(
)(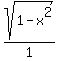 ) = 1
Clear of fractions by multiplying through by LCD 5
x +
) = 1
Clear of fractions by multiplying through by LCD 5
x + 
 = 5
Isolate the radical term:
= 5
Isolate the radical term:

 = 5 - x
Square both sides of the equations:
24(1 - x²) = (5 - x)²
24 - 24x² = (5 - x)(5 - x)
24 - 24x² = 25 - 10x + x²
Get 0 on the right:
25x² - 10x + 1 = 0
Factor the left side:
(5x - 1)(5x - 1) = 0
(5x - 1)² = 0
5x - 1 = 0
5x = 1
x =
= 5 - x
Square both sides of the equations:
24(1 - x²) = (5 - x)²
24 - 24x² = (5 - x)(5 - x)
24 - 24x² = 25 - 10x + x²
Get 0 on the right:
25x² - 10x + 1 = 0
Factor the left side:
(5x - 1)(5x - 1) = 0
(5x - 1)² = 0
5x - 1 = 0
5x = 1
x =  Edwin
Edwin