Question 629131: log2(x-1)+ log2 (x-4)=log2(2x-6)?what is the answer?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume that the equation is:

and not

or

Posting logs with bases other than 10 or e is difficult. If you are going to post more problems like this, then you might want to click on the "Show source" link above to see what I type to get these logs to display the way you see here.
Solving equations where the variable is in the argument of one or more logarithms usually starts with using algebra and/or properties of logarithms to transform the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
Since the terms of your equation are all logarithms, the second, "all-log" form will be easier to achieve. All we have to do is find a way to combine the two logs on the left side into one (or find some other way to make one of the logs disappear). There are two ways to combine logs:- Add or subtract them if they are like terms. Like logarithmic terms have the same bases and the same arguments.
- Use one of the following properties of logarithms:
Your logs have the same base, 2. but they have different arguments, x-1 and x-4, so we will not be able to add them together.
Your logs have the same base and their coefficients are 1's so we will be able to use the properties to combine them. We use the first property because its logs, like ours, have a "+" between them:

which simplifies (using FOIL on (x-1)(x-4)) to:

We now have the desired form.
The next step is based on some simple logic. Logarithms are exponents. With a base of 2, our logarithms are exponents to put on a 2. The equation says that these to two exponents for a 2 are equal. And when you raise 2 to some power there is only one result. So when we raise 2 to either the 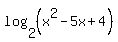 power we should get the same thing as when we raise 2 to the power we should get the same thing as when we raise 2 to the 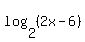 power since the exponents are the same! So: power since the exponents are the same! So:

We now have an equation we can solve. It is quadratic so we want one side to be zero. Subtracting 2x and adding 6 we get:

Next we factor or use the Quadratic Formula. This factors easily:

From the Zero Product Property we know that one of these factors must be zero:
x-5 = 0 or x-2 = 0
Solving these we get:
x = 5 or x = 2
When solving logarithmic equations like these we must check our solutions. It is not optional! You must ensure that all arguments to all logs remain positive for each solution you found. If you find that a "solution" makes an argument of a log zero or negative, then you must reject/discard that solution.
Use the original equation to check:

Checking x = 5:

Simplifying:

We can now see that all three arguments are positive. So this solution checks out.
Checking x = 2:

Simplifying:

We can see that two arguments are negative. So we must reject this solution.
So the only solution to your equation is: x = 5
|
|
|