Question 628722: Can someone please help me solve this equation: log(b) sqrt (x)*y^2 / z^2
How do I use the properties of logarithms to expand this expression as a sum, difference, or possibly as a constant of multiples of logarithms. Thanks.
- Cassidy
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! For these kinds of problems you use the following properties of logarithms:- To separate products in the argument:
 - To separate a fraction/division in the argument:
 - To move an exponent of of the argument:

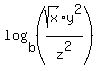
Note: if your expression is not the above but 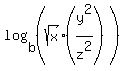 : :- The answer happens to work out the same.
- Use parentheses to enclose numerators in the future. This problem happens to work out the same whether the square root is in front of the fraction or if it is in the numerator. But not all problems will work out the same either way. So make your postings clear and accurate by using using parentheses freely, especially around numerators, denominators, entire fractions, exponents, arguments to functions, and expressions inside a radical.
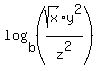
The argument is, in essence, a fraction. So we use the second property above to split it apart:

The argument of the first log is, in essence, a product. So we use the first property to split it apart:

Since square roots are equal to exponents of 1/2, all three of the logs have exponents on their arguments. We use the third property to move the exponent out in front of the logs:
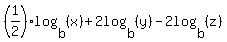
And we're finished!
|
|
|