Question 628629: Two trains start from P and Q respectively and travel towards each other at a speed of 50 km/hr and 40 km/hr respectively. By the time they meet, the first train has traveled 100 km more than the second. Find the distance between P and Q.
Need answer with solution urgently.. Thanks a million..
Found 2 solutions by richwmiller, MathTherapy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two trains start from P and Q respectively and travel towards each other at a speed of 50 km/hr and 40 km/hr respectively. By the time they meet, the first train has traveled 100 km more than the second. Find the distance between P and Q.
Need answer with solution urgently.. Thanks a million..
Let distance traveled by faster train be D
Then distance traveled by slower train = D - 100
Time taken by faster train to travel to meeting point = time taken by slower train to travel to the meeting point, OR

50(D – 100) = 40D ------ Cross-multiplying
50D – 5,000 = 40D
50D - 40D = 5,000
10D = 5,000
D, or distance traveled by faster train = 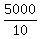 , or , or  km km
Distance traveled by slower train = 500 – 100, or  km km
Therefore, distance between P and Q = 500 + 400, or  km km
You can do the check, I'm sure!!
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|