SOLUTION: The attendance for a week at a local theatre is normally distributed, with a mean of 4000 and a standard deviation of 500. Draw the normal curve to represent the normally distribut

Click here to see ALL problems on Probability-and-statistics

Question 628483: The attendance for a week at a local theatre is normally distributed, with a mean of 4000 and a standard deviation of 500. Draw the normal curve to represent the normally distributed attendance for the week. What percentage of the attendance would be less than 3500? What percentage of the attendance would be greater than 5000? What percentage of the attendance figures would be between 3700 and 4300 each week?
Am I supposed to try and solve this from the graph or can it be calculated?
Thank you for your help.
Answer by ewatrrr(24785) (Show Source):
You can put this solution on YOUR website!

Hi,
mean of 4000 and a standard deviation of 500
Important to Understand z -values as they relate to the Standard Normal curve:
Below: z = 0, z = � 1, z= �2 , z= �3 are plotted.
Note: z = 0 (x value the mean) 50% of the area under the curve is to the left and 50% to the right

This curve alone does not give exact percentages with the exception of P(z=0) = .50 or 50%
A Pictorial where 'some' of the % have been added for helps more...
However, most often one needs to use a table, calculator, or an Excel function ect to find exact Percentage,
after finding z:

P(x < 3500) = P(z = (3500-4000)/500) = P(z = -1) = 1 - () = 1 - (.5 +.341) = 1-.841 = .159 or 15.9% |using above pictorial
P(x > 4000) = P(z = 0) = .50 or 50 % |using above pictorial
P(3700< x < 4300) = P( - z =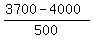) = P( - )
Using Calulator etc: Here, am using the Excel NORMSDIST function to find the Percenatges:
P( - ) = .7257 - .2742 =.4515 or 45.15%