|
Question 628327: how do you graph x<6y-y^2
Found 2 solutions by jsmallt9, Edwin McCravy:
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! First, draw the graph of the corresponding equation:  . IMPORTANT: Draw the graph as a dotted curve, not a solid one as you do with equations. The reason we do this is: A solid curve represents all the points where the x coordinate equals  . But our inequality says that the x is less than but not equal to . (If the inequality had been  we would use a solid curve because we would want to include the points where the x coordinate is equal to ).
If you know your conic sections, then you should recognize that:- is the equation of a parabola.
- This parabola will open horizontally (sideways) because y is squared, not the x.
- This parabola will open to the left because of the negative in front of the
 .
I will leave the specifics up to you. But you should end up with a dotted parabola that opens to the left.
Second, we must determine where to shade the graph. Our dotted, leftward-opening parabola, in effect, divides the plane into two parts: The part inside the "bowl" of the parabola and the part outside the bowl. We will shade one of these two parts. But which part? There are two ways to figure this out:- The inequality says x is less than . Where do we find smaller x's? To the left or to the right? It should be well-known that smaller x's are to the left. And if we start at any point on our parabola (where
 ) and go left (where the smaller x's are) where to we end up? Inside or outside the bowl of the parabola? No matter which point on the parabola you start from, going left should put you inside the bowl. So this is where we shade: inside the bowl. - Determine the coordinates of any point that is unquestionably inside or outside the bowl. (In this case something to the right of the vertex is safe.) Insert these coordinates into your inequality,
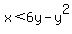 , and see if the coordinates fit (i.e. make it a true statement. If the coordinates fit then shade the area that include the point you chose. If the coordinates do not fit, then shade the area that does not include the point you chose. (If you chose a point to the right of the vertex, the coordinates should not fit your inequality and so we should shade the other area, the area inside the bowl.
So either way we should find that shading the inside of the bowl is correct.
In summary, your graph should be a dotted, leftward-opening parabola with its inside shaded.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
x < 6y - y²
Graph the boundary curve by replacing the < by =
x = 6y - y²
y² - 6y = -x
Complete the square on the left by adding ( ·(-3)² = 9
to both sides:
y² - 6y + 9 < -x + 9
Factor the left side
(y - 3)² = -x + 9
This is in the form of a parabola with
horizontal line of symmetry
(y - k)² = 4p(x - h)
(y - 3)² = -1(x - 9)
The vertex is (h,k) = (9,3) and it opens left since 4p = -1
p =  which is negative:
You can get a few points in addition to the vertex, say
(5,5), (5,1), (0,6), (0,0), (-7,7), (-7,-1)
Now the question is whether to shade the inside portion or the outside
portion of the parabola. So we test a point that's not on the parabola,
say (3,4), which is inside the parabola, in the original inequality:
We substitute that into the original inequality:
x < 6y - y²
3 < 6(4) - (4)²
3 < 24 - 16
3 < 8
This is true, so since (3,4) is a solution and it is on the
inside of the parabola, all the points inside the parabola
are solutions.
Edwin
|
|
|
| |
