Question 62827: Please help me solve this problem:
x+1 divided by x-1 is greater than or equal to 0
Answer by funmath(2933)   (Show Source):
You can put this solution on YOUR website! Please help me solve this problem:
Your intervals to test are found by finding what makes the fraction =0, by finding what makes the numerator=0.
x+1=0
x+1-1=0-1
x=-1
and what makes the fraction undefined, what makes the denominator=0.
x-1=0
x-1+1=0+1
x=1 Keep in mind that x cannot=1
The possible intervals to our solution are:
(-infinity,-1], [-1,1), (1,infinity)
Test a point in the interval (-infinity,-1], like -2.
 This is true, so (-infinity,-1] is part of the solutuion.
Test a point in the interval [-1,1), like 0.
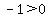 This is false, so the interval [-1,1) is NOT part of the solution.
Finally test a point in the interval (1,infinity), like 2.
 is true, therefore the interval (1,infinity) is part of the solution.
Therefore the solution is:
(-infinity,-1]U(1,infinity)
Happy Calculating!!!
|
|
|
