|
Question 628133: graph R(x) = x^4+x^2+5/x^2-36
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
If you are in or have taken a Calculus class then you should mention this. Graphing these kinds of functions is easier if you can use some Calculus. I'm not going to use Calculus in the following but I will, at the end, tell you what to do if you know it.
First let's notice that all the exponents on x are even. This means that the graph of R(x) will be symmetric to the y-axis. IOW, THe graph to the right of the y-axis will be a mirror image of the graph to the left of the y-axis.
Next, let's determine the vertical asymptotes. Vertical asymptotes occur for x values, if any, that make the denominator zero. To find them we set the denominator equal to zero and solve for x:

Solving this you should find that x = 6 or x = -6. This are the equations of the two vertical asymptotes of R(x). Because of the symmetry, we should not be surprised with the symmetry of the asymptotes.
Next, let's look for horizontal asymptotes. Horizontal asymptotes occur if the value of the function approaches some value(s) for very large positive or negative values. In order for horizontal asymptotes to occur the degree of the numerator must be less than or equal to the degree of the denominator. Your numerator has a degree of 4 and your denominator has a degree of 2. So there will not be any horizontal asymptotes for R(x).
Even though there are no horizontal asymptotes we can still consider what happens to R(x) for large positive and negative values of x. For this it can be helpful to use long division to actually divide the numerator by the denominator. Using long division on R(x) we get:

For very large values of x, positive and negative the denominator of the fraction will be very large. Fractions with very large denominators have very small, near zero, values (even with a numerator of 1337). So for large x's, R(x) will have a value very near the value of 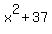 . And . And 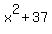 will have very large positive values for large x's. In summary, R(x) will have very large positive values (way up high on the graph) for both large positive x's (on the right) and large negative x's (on the left). will have very large positive values for large x's. In summary, R(x) will have very large positive values (way up high on the graph) for both large positive x's (on the right) and large negative x's (on the left).
Now let's analyze R(x)- The numerator, because the x's have even exponents and the 5 is positive, will never be zero or negative. Since the numerator is always positive we know two things:
- R(x) will never be zero. This means that the graph of R(x) will never cross the x-axis.
- The sign of R(x) will be determined solely by the sign of the denominator.
- The denominator will be positive if
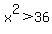 and it will be negative if and it will be negative if  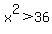 if x > 6 or if x < -6 if x > 6 or if x < -6 if x is between -6 and 6 if x is between -6 and 6
So the denominator will be positive if x > 6 or if x < -6 and it will be negative if x is between -6 and 6. And since the sign of the denominator is deciding the sign of R(x), R(x) will be positive when x > 6 or x < -6 and negative for x's between -6 and 6.
Let's summary all that we have found:- The graph of R(x) never crosses the x-axis (because the numerator can never be zero).
- R(x) has two vertical asymptotes: x = -6 and x = 6.
- These vertical asymptotes will divide the graph into three parts:
- To the left of x = -6. In this area, x < -6 which makes R(x) positive. So the graph will be above the x-axis (positive) in this entire section. We have also learned that large negative x's (way off to the left, R(x) has vary large (way up high) values. Since R(x) never crosses the x-axis, R(x) must also go way up high as it approaches the asymptote x = -6 from the left side. All together, R(x) will have a "u-ish" shape, all above the x-axis in this section.
- In between the asymptotes. Here the denominator is negative and so is R(x). So R(x) will be below the x-axis in this entire section. So R(x) must approach the two asymptotes "way down low". Because of the symmetry, R(x) has literally an upside-down U shape, all below the x-axis in this section.
- To the right of x = 6. we should get a mirror image of the section to the left of x = -6.
If you know some Calculus you would find the first and second derivatives to find the "bottom" of each of the u-ish shapes and to find wobbles, if any, in the curve.
And finally, with or without the Calculus, you can "flesh out" all of this by actually finding points on the graph. Pick some numbers for x (anything except 6 or -6) and find the value of R(x) for those x's. Each of these pairs will be coordinates of a point on the graph of R(x).
You should get something like:

Notes:- Algebra.com's graphing software is not perfect. It may look like the graph actually touches the asymptotes, even though it should not. It may also look like the graph touches/crosses the x-axis near the origin, even though R(x) will not.
- The scale on the y-axis is different than the scale on the x-axis. I did this on purpose so it would be easier to see some of the graph of R(x)
|
|
|
| |