Here is how to do it in your head:
In 30 hours the first hose could fill 2 pools and the second one could
fill 3 pools, so together in 30 hours both could fill 5 pools, so together
they could fill 1 pool in only 6 hours.
Here is how to do it with algebra. Make this chart:
no. of pools filled time rate in pools/hour
1st hose
2nd hose
both together
Put x for the time for both together, 15 and 10 for the times for each
hose separately, and 1's for the no. of pools, since doing it this way
we are only interested in 1 pool being filled.
no. of pools filled time rate in pools/hour
1st hose 1 15
2nd hose 1 10
both together 1 x
Now fill in the three rates by dividing pools by hours:
no. of pools filled time rate in pools/hour
1st hose 1 15 1/15
2nd hose 1 10 1/10
both together 1 x 1/x
The equation comes from
+ 
= 
+ 
= 
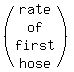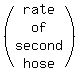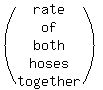
Multiply through by LCD of 30x
2x + 3x = 30
5x = 30
x = 6
Answer: 6 hours. Same as when you do it in your head.
Edwin
