Question 627545: while walking by a farmyard filled with chicken and rabbits, a farmer decided to count the heads and feet of his animals. He came up with a sum of 100 ( counting both heads and feet). How many of each animals where in the farmyard?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Usually, problems of this type give you as many pieces of information as the number of variables you have to solve for.
That way you can set up a system of linear equations that could have one unique solution.
When you have a system of linear equations with more variables than equations,
there could be more than one solution.
If the only information you have is a total count of heads plus feet,
you just have one linear equation with two variables.
One linear equation with two variables graphs as a straight line,
and all the points in the line represent solutions.
In general, that would give you infinite solutions.
In this case, you need the numbers of chickens and rabbits to be integers,
so there is a finite number of solutions
Let  be the number of chickens and let be the number of chickens and let  be the number of rabbits. be the number of rabbits.
The number of heads plus feet for  chickens is chickens is 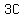 . .
The number of heads plus feet for  rabbits is rabbits is 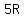 . .
The total number of heads plus feet for  chickens and chickens and  rabbits is rabbits is
 . .
Because  and and  are non-negative integers, are non-negative integers,
the linear equation above has only a few solutions.
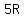 and and  are multiples of 5, are multiples of 5,
so 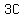 must also be a multiple of 5, must also be a multiple of 5,
which means that  must be a multiple of 5. must be a multiple of 5.
From the wording you posted, I would expect one or more chickens, but interpretations may vary.
For a math teacher  with with  (zero chicken, just 20 rabbits) could be a possibility. (zero chicken, just 20 rabbits) could be a possibility.
There are other possibilities that everyone would agree about.
There could be 5, 10, 15, 20, 25, or 30 chickens.
(35 chickens would have too many heads plus feet).
For each possible value of  , ,
we can find a value for  from the equation from the equation  . .
For example:
for  , ,  --> -->  --> -->  --> -->  --> -->  --> -->  , ,
for  , ,  --> -->  --> -->  --> -->  --> -->  --> -->  , ,
and so on.
The solutions, written as ordered pairs (C,R) are:
(0,20), (5,17), (10,14), (15,11), (20,8), (25,5), and (30,2).
We can graph the equation (line) and the solutions (circled points) as follows:

|
|
|