The graph of
y =  |x - 4| - 5
can be obtained from the graph of
y = |x| as follows:
|x - 4| - 5
can be obtained from the graph of
y = |x| as follows:
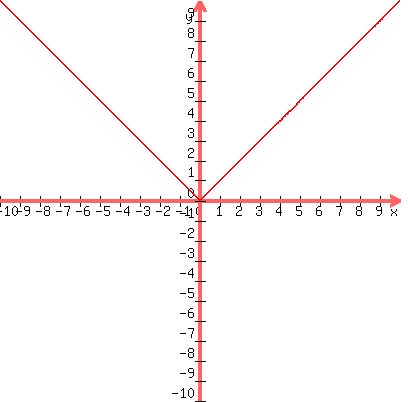 , which is the graph of y = |x| to this:
, which is the graph of y = |x| to this:
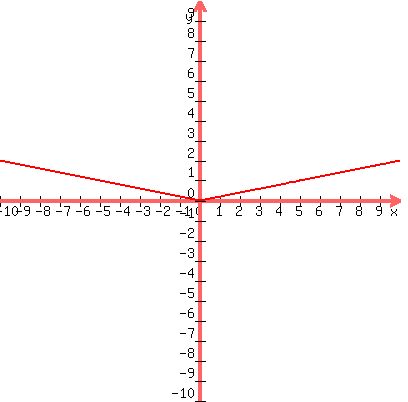 , which is the graph of y =
, which is the graph of y =  |x| the above graph shrunk vertically by a factor or
|x| the above graph shrunk vertically by a factor or  to this:
to this:
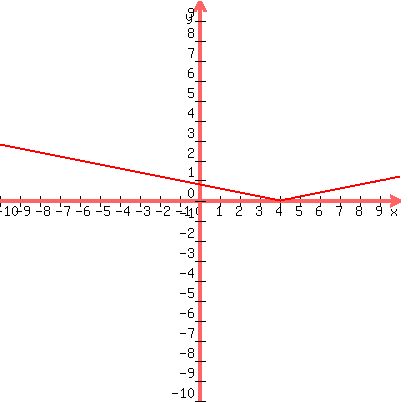 , which is the graph of y =
, which is the graph of y =  |x - 4|, the above graph shifted horizontally right 4 units to this:
|x - 4|, the above graph shifted horizontally right 4 units to this:
 , which is the graph of y =
, which is the graph of y =  |x - 4|-5, the above graph shifted vertically down 5 units.
There is no reflecting in either axis.
Edwin
|x - 4|-5, the above graph shifted vertically down 5 units.
There is no reflecting in either axis.
Edwin