Question 62663: Please help me solve this question. What is the average of 3^22, 3^23 and 3^24
Found 3 solutions by joyofmath, uma, jai_kos:
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me solve this question. What is the average of 3^22, 3^23 and 3^24
Let the three numbers to average be a, b, and c.
So,  . .
Then  . .
Also,  . .
So,  and and  . .
So, the three numbers to average, in terms of a, are a, 3*a, and 9*a.
You get the average of three numbers by adding them up and dividing by 3.
So, the average is:  . .
Put  back into the equation and the average is: back into the equation and the average is: 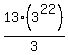 . .
But,  so the average is so the average is 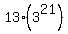 . .
Answer by uma(370)   (Show Source): (Show Source):
You can put this solution on YOUR website! The average of any set of numbers is = sum of the numbers/No: of values
So the average of 3^22, 3^23, 3^24 = (3^22 + 3^23 + 3^24)/3
= (3^22 + 3*3^22 + 3*3*3^22)/3
= 3^22(1 + 3 + 9)/3
= 3^22(13)/3
= 3^21(13) [when divided, the exponents are subtracted]
So the average = 13(3^21)
Good Luck!!!
Answer by jai_kos(139)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given 3^22, 3^23 and 3^24
We find that the base is same, only the powers are different.
3^22 + 3^23 + 3^24 = 3^ (22 + 23 + 24)
= 3^ (69)
THe average is given by the total number divide the number of terms.
Average = 3 ^ 69 / 3 ^ 3
Since there are 3 terms.
Average = 3 ^ (69 / 3)
= 3 ^ 23
Therefore the average is given by 3 ^ 23
|
|
|