Suppose that you have 8 cards. 5 are green and 3 are yellow. The 5 green cards are numbered 1, 2, 3, 4, and 5. The 3 yellow cards are numbered 1, 2, and 3. The cards are well shuffled. You randomly draw one card.
• G = card drawn is green
• Y = card drawn is yellow
• E = card drawn is even-numbered
List: 1)sample space
{G1,G2,G3,G4,G5,Y1,Y2,Y3}
----------------------------------------
2)Enter probability P(G) as a fraction.
There are 5 G's out of 8 cards, so the probability is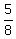 
----------------------------------------
3)P(G|E)
We can do this one either of two ways. Either way gives the same answer.
First way: Reduce the sample space to what is given. Since we are given
E, we reduce the sample space to just those with even numbers, so we
delete everything from the sample space in problem 1) that doesn't have
an even number, and keep only the ones which do. So the reduced sample
space is {G2,G4,Y2}. Now P(G|E) = P(G) using the reduced sample space.
Thats 2 out of 3 or 
.
Second way: Use the formula for conditional probability:
P(G|E) = 
= 
= 
= 
= 
=
----------------------------------------
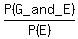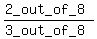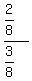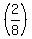
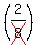
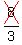4)P(G AND E)
There are 2 ways, G2 and G4, to have both Green AND Even out of 8 ways, so
the probability P(G AND E) = 
= 
----------------------------------------
5)P(G or E)
There are 6 ways, G1,G2,G3,G4,G5 or Y2 to have one OR the other of either
Green OR Even. So the probability is 
which reduces to 
.
----------------------------------------
6)Are G and E are mutually exclusive
Think of the word "exclusiVE" as "excludiNG". They do not EXCLUDE each other.
They are not mutually exclusive events because to be mutually exclusive events,
the two events must be such that if one of them is true the other MUST BE
false. In other words, the truth of one would have to EXCLUDE the other.
Here Green does not EXCLUDE Even, because for instance, we could
draw G2.
----------------------------------------
Edwin
