|
Question 625894: A. Graph the function ƒ(x) = x3 - 4x + 2.
B. Find the domain and range of ƒ, showing all work or explaining your rationale.
C. Find the derivative of ƒ, showing all work.
D. Find the slope of the graph of ƒ at x = 0, showing all work.
E. Let ƒ represent the position of an object with respect to time that is moving along a line. Identify when the object is moving in the positive and negative directions and when the object is at rest, showing all work.
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20062)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A. Graph the function ƒ(x) = x³ - 4x + 2.
 B. Find the domain and range of ƒ, showing all work or explaining your rationale.
ƒ(x) is a polynomial function of odd degree.
All polynomial functions are defined for all values of x and have domain
(
B. Find the domain and range of ƒ, showing all work or explaining your rationale.
ƒ(x) is a polynomial function of odd degree.
All polynomial functions are defined for all values of x and have domain
( , , )
All odd degree polynomial functions have both domain and range
( )
All odd degree polynomial functions have both domain and range
( , , ).
C. Find the derivative of ƒ, showing all work.
ƒ(x) = x³ - 4x + 2
ƒ'(x) = 3x² - 4
D. Find the slope of the graph of ƒ at x = 0, showing all work.
ƒ(x) = x³ - 4x + 2
ƒ'(x) = 3x² - 4
ƒ'(0) = 3(0)² - 4
ƒ'(0) = -4
The slope of the graph at x = 0, which is the slope of the
green line below which is tangent to the curve at (0,2) ).
C. Find the derivative of ƒ, showing all work.
ƒ(x) = x³ - 4x + 2
ƒ'(x) = 3x² - 4
D. Find the slope of the graph of ƒ at x = 0, showing all work.
ƒ(x) = x³ - 4x + 2
ƒ'(x) = 3x² - 4
ƒ'(0) = 3(0)² - 4
ƒ'(0) = -4
The slope of the graph at x = 0, which is the slope of the
green line below which is tangent to the curve at (0,2)
 E. Let ƒ represent the position of an object with respect to time that is moving along a line. Identify when the object is moving in the positive and negative directions and when the object is at rest, showing all work.
ƒ(x) = x³ - 4x + 2
E. Let ƒ represent the position of an object with respect to time that is moving along a line. Identify when the object is moving in the positive and negative directions and when the object is at rest, showing all work.
ƒ(x) = x³ - 4x + 2
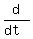 f(x) = 3x² f(x) = 3x²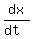 - 4 - 4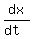 f(x) = (3x² - 4) f(x) = (3x² - 4)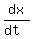 }
The object is moving in the positive direction when 3x² - 4 > 0. That is,
Find critical numbers of 3x² - 4
3x² - 4 = 0
3x² = 4
x² = }
The object is moving in the positive direction when 3x² - 4 > 0. That is,
Find critical numbers of 3x² - 4
3x² - 4 = 0
3x² = 4
x² =  x =
x = 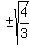 x =
x = 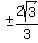 approximately ±1.1545
These critical numbers are when the object is at rest, because
the derivative of f with respect to time is 0 there.
Choose test value -2 which is less that approximately ±1.1545
These critical numbers are when the object is at rest, because
the derivative of f with respect to time is 0 there.
Choose test value -2 which is less that  Substitute in 3x² - 4
3x² - 4
3(-2)² - 4
3(4) - 4
12 - 4
8
That's positive, so the object is moving in the positive direction
when x <
Substitute in 3x² - 4
3x² - 4
3(-2)² - 4
3(4) - 4
12 - 4
8
That's positive, so the object is moving in the positive direction
when x <  Choose test value 0 which is between the two critical numbers
Choose test value 0 which is between the two critical numbers
 and and  Substitute in 3x² - 4
3x² - 4
3(0)² - 4
-4
That's negative, so the object is moving in the negative direction
when
Substitute in 3x² - 4
3x² - 4
3(0)² - 4
-4
That's negative, so the object is moving in the negative direction
when  < x < < x <  Choose test value 22 which is greater that
Choose test value 22 which is greater that  Substitute in 3x² - 4
3x² - 4
3(2)² - 4
3(4) - 4
12 - 4
8
That's positive, so the object is moving in the positive direction
when x >
Substitute in 3x² - 4
3x² - 4
3(2)² - 4
3(4) - 4
12 - 4
8
That's positive, so the object is moving in the positive direction
when x >  Answer:
The object is moving in the positive direction when
x <
Answer:
The object is moving in the positive direction when
x <  and when x > and when x >  The object is moving in the negative direction when
The object is moving in the negative direction when
 < x < < x <  The object is at rest when x =
The object is at rest when x =  and when x = and when x =  Edwin
Edwin
Answer by AnlytcPhil(1807)   (Show Source): (Show Source):
|
|
|
| |